Когда я думаю о задаче, которая касается степеней и логарифмов, я задаю себе два вопроса:
Речь идет о вводных параметрах (то, что вызвало конечное изменение) или о результате (собственно, произошедшем изменении)?
- Логарифмы раскрывают именно аргументы (входные параметры), которые вызвали рост
- Степени помогают вычислить конечный результат роста
Мы смотрим на задачу с позиции объекта роста или наблюдателя этого процесса?
- e и натуральный логарифм отражают рост с позиции объекта роста.
- Основание 10, основание 2 и т.д. — это измерения, удобные для наблюдателя.
В своей голове я упорядочиваю всё в таблицу:
| Найти причину | Найти следствие | |
|---|---|---|
| С точки зрения растущего | ln(x)натуральный логарифм | exэкспонента с основанием e |
| С точки зрения наблюдателя | log10(x), log2(x)другие логарифмы | 10x, 2xдругие экспоненты |
У меня появляются мысли вроде «Мне нужна причина, с точки зрения того, кто растет… это натуральный логарифм.». (Натуральный логарифм на латыни звучит как logarithmus naturalis, отсюда пошло и сокращение, используемое в математике, — ln).
Я очень не любил уроки, на которых преподаватель описывал содержимое таблицы, эти функции, без каких-либо пояснений, когда и как их нужно применять!
Такой подход, увы, не срабатывает. Давайте попрактикуемся в том, как мыслить логарифмами и степенями, на реальных примерах.
Пример №1: Описание роста ВВП
Вот типичный пример роста:
- С 2000 по 2010 год ВВП страны изменился с 9,9 триллионов до 14,4 триллионов монет.
Хорошо, эти цифры показывают уже произошедшее изменение. Но нам бы, возможно, хотелось узнать составные части такого изменения: Какой средний ежегодный прирост привел к такому конечному изменению? И тут же мой мозг подсказывает мне: «логарифмы», потому что мы задаемся вопросом, что вызвало такой конечный рост. В голове срабатывает схема:
логарифм изменения → источник роста
Неплохой старт, но давайте его немного дополним.
Для начала, какой логарифм нам использовать?
По умолчанию я выбираю натуральный логарифм. Большинство событий касаются непосредственно предмета роста (а не наблюдателя), и я люблю «идти рядом» с растущим объектом, чтобы визуализировать происходящее. (Так же и с радианами: они измеряют углы с позиции того, кто движется).
Следующий вопрос: к какому изменению применить логарифм?
Мы всего лишь заинтересованы в отношении между стартом и финишем: 9,9 миллиардов к 14,4 миллиардам за 10 лет. Это такой же коэффициент роста, как если вырасти с 9.9 монет до 14.4 монет за тот же период времени.
Мы можем отточить нашу первоначальную мысль:
натуральный логарифм доли роста → источник роста
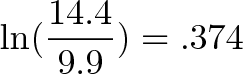
Хорошо, источником роста послужил коэффициент в 0,374 или 37,4%. Мы закончили?
Еще нет. Логарифмы ничего не знают о том, сколько времени понадобилось на такое изменение (мы же не включили в расчет 10 лет, верно?). У нас получился коэффициент, как если бы всё изменение целиком произошло за 1 единицу времени.
Такой прирост в 37,4% действительно мог случиться за один год, или за два года равномерного роста на 18,7%, или из любой другой комбинации.
По сценарию мы знаем, что изменение произошло за 10 лет, и коэффициент этого изменения должен быть:
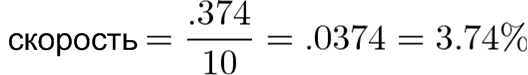
С точки зрения постоянного, равномерного роста, экономика страны росла на 3,74% ежегодно.
Теперь мы закончили? Еще нет!
Этот постоянный коэффициент рассчитан с позиции растущего объекта (т.е. ВВП), как если бы мы постоянно шли рядом с экономикой на графике, пока она изменялась. Банкиру, вероятно, хотелось бы знать ежегодную разницу в приросте. Мы можем рассчитать этот показатель, дав постоянному росту поработать годик:
экспонента со скоростью и временем → эффект от роста

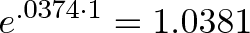
Ежегодный прирост составил 3,8%, немного выше, чем 3,74% — мгновенный коэффициент, без учета роста самого прироста. Получается, что:
- Данная часть экономики номинально растет на 3,74% , этот рост смоделирован функцией e0,0374 × годы
- Если считать по ежегодному базису, когда срабатывает составной рост ВВП (образовавшаяся часть прироста дает свой собственный прирост), то общий прирост составит уже 3,81%, смоделированный функцией 1,0381годы
В финансах актуальнее исследовать изменения по сравнению с предыдущим годом, которые можно сравнивать с другими трендами. В науке и технике предпочтительнее моделировать текущее поведение, исследуя мгновенные изменения.
Пример №2: Описание естественного роста
Я ненавижу надуманные примеры вроде «Предположим, что количество бактерий удваивается каждые 24 часа, вычислите формулу их роста». Неужели колонии бактерий размножаются четко по человеческим часам, и к конкретному времени мы ожидаем точное удвоение популяции?
Вот сценарий получше: «Я нашел немного бактерий, подождал часок, и в результате их общая масса увеличилась с 2,3 до 2,32 граммов. Сейчас я иду на обед. Вычислите, какое количество бактерий будет через 3 часа, когда я вернусь».
Давайте смоделируем эту ситуацию. Нам нужен логарифм для вычисления коэффициента роста, а затем степень, чтобы спроектировать будущий рост. Как и в предыдущий раз, давайте для начала придерживаться натуральных логарифмов.
Фактор роста таков:
логарифм изменения → источник роста
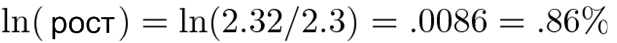
Это и есть коэффициент роста за один час, и общая модель будущего роста будет:
экспонента со скоростью и временем → эффект от роста
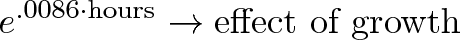
Если на старте у нас 2,32 грамма, то рост за 3 часа будет:
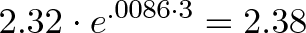
Ну и из спортивного интереса, через какое время бактерии удвоятся в количестве? Представьте, что мы ждем, пока 1 превратится в 2:

Мы можем механически вычислить натуральный логарифм обеих сторон уравнения, чтобы «отменить экспоненту», но давайте мыслить интуитивно.
Если 2 — это конечный результат, то ln(2) — это рост, который привел нас к этому результату (какой-то коэффициент x время). Мы знаем, что коэффициент равен 0,0086, так что время роста до 2 будет таким:
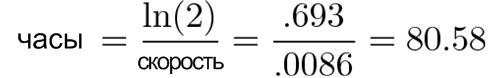
Колония удвоится через ~80 часов. (Не пропало желание дождаться этого результата?)
Что в действительности означает смена перспективы?
Выбор поиска входной величины (источника роста) или исхода (результат роста) очень прост. Но как Вы визуализируете процесс с точки зрения объекта роста?
Представьте, что у нас есть два маленьких работника, которые строят финальную модель роста (помните графики из статьи про экспоненты и число е, где деньги были как пример?)
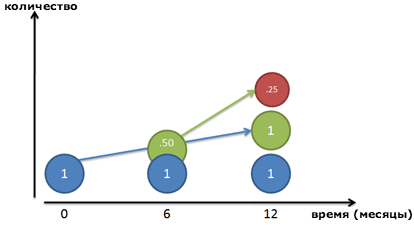
Если коэффициент роста 100%, мы говорим нашему работнику (синий кружок) работать старательно и создать 100% копию себя самого к концу года (зеленый кружок).
Но… новый работник (зеленый кружок) тоже начинает работать. Если Зеленый впервые появляется на графике на отметке в 6 месяцев, у него есть еще полгода на работу (при таком же ежегодном коэффициенте роста, как и Синего). Зеленый человечек начинает создавать Красного. Конечно, Красный будет сделан только наполовину к концу срока, потому что у Зеленого было в запасе только полгода.
А что, если Зеленый впервые появился не через полгода, а через 4 месяца? Месяц? День? Секунду? Если работники начали работу сразу, то у нас будет кривая мгновенных изменений, определенная ex:
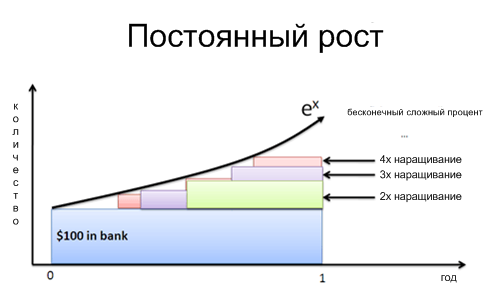
Натуральный логарифм дает нам коэффициент роста с точки зрения того самого «человечка». Мы включаем этот коэффициент в ex, чтобы найти конечный результат, включая все составные роста.
Использование других оснований
Переключение на другой тип логарифма (с основанием 10, с основанием 2 и т.д.) означает, что мы ищем определенную закономерность в общем росте, а не что-то, касающееся конкретного работника. Каждый логарифм задается своим вопросом, когда происходит изменение:
- Логарифм с основанием e: Какова мгновенная скорость работы каждого работника?
- Логарифм с основанием 2: Как много удвоений требуется?
- Логарифм с основанием 10: Сколько удесятерений требуется?
Вот небольшой пример для анализа:
- За последние 30 лет количество транзисторов в типичных микросхемах увеличилось с 1000 до 1 миллиарда.
Как вы это проанализируете?
- Все эти микросхемы — это не совокупная единица, которая плавно растет с течением времени. Это разные схемы, произведенные разными конкурирующими компаниями, которые в совокупности определяют общий тренд развития.
- Так как мы не «идем рядом» с расширяющейся микросхемой, давайте использовать масштаб, созданный для удобства человека, чтобы проанализировать такой рост. Об удвоении как-то проще размышлять, чем об удесятерении, так что с него и начнем.
Получаем:
логарифм изменения → источник роста
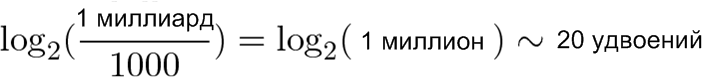
«Источником роста» послужили 20 удвоений, которые, как мы знаем, произошли в течение 30 лет. В среднем это 2/3 удвоений за год или 1,5 года на каждое удвоение.
С позиции растущего объекта, мы вычислим ln(1 миллиард/1000)/30 лет=46% непрерывного роста (такой рост немного сложно представить в контексте данного примера). Мы можем резюмировать наш анализ в таблицу:
Ситуация: от тысячи к 1 млрд транзисторов за 30 лет
| Найти причину | Найти следствие | |
|---|---|---|
| С точки зрения растущего | ln(1 млрд/1000) = 13.8113.81 входящей причины / 30 лет = коэффициент 0.46 в годнайти коэффициент непрерывного роста | e0.46 × годыпромоделировать непрерывный рост |
| С точки зрения наблюдателя | log2(1 млрд/1000) = 20 удвоений20 удвоений / 30 лет = 2\3 удвоения в годнайти коэффициент роста удвоениями | 22\3 × годыпромоделировать рост удвоениями |
Заключение
Изучение — это процесс поиска скрытого смысла за определенным понятием. Когда это понятие используется? С какого угла нужно посмотреть на задачу?
Данная интерпретация говорит о том, что показатели степени как бы спрашивают — причина или результат, объект роста или наблюдатель роста? Именно это и помогает мне понять суть логарифмов и степеней.
Приложение: Изменение базовой формулы
Вот как можно пояснить смену оснований. Взяв 100% непрерывный показатель прироста:
- ln(x) — это время роста до x
- ln(2) — это время роста до 2
Так как на удвоение у нас уйдет определенное время, мы можем вычислить, как много удвоений «поместится» в общее время роста до x:
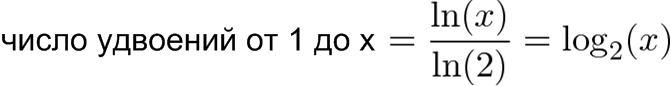
Например, сколько удвоений происходит с 1 до 64?
Ну, ln(64)=4,158. А ln(2)=0,693. Количество удвоений равно:
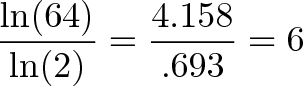
В реальном мире калькуляторы могут быть не точными, так что по возможности используйте функцию логарифма с основанием 2. И, конечно, у нас может получиться дробное число: рост с 1 до квадратного корня 2 — это «половина» удвоения, или log2(1.414) = 0,5. Переход к логарифму с основанием 10 означает, что мы подсчитываем количество удесятерений, которое «помещается» в рост с 1 до х:
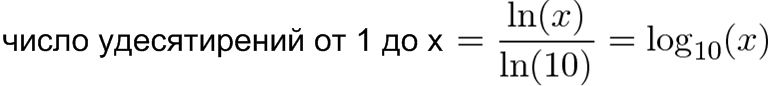
Здорово, правда?
Приятных вам вычислений!
Перевод статьи «How To Think With Exponents And Logarithms»

