Что такое синус и синусоида

Синусоиды всегда меня смущали. Можно бесконечно рисовать треугольники и повторять теоремы наизусть. Но что они означают?

Я зашел в тупик, пытаясь извлечь синус из других форм. Быстрая аналогия:

Вы: Геометрия описывает формы, линии и т.д.
Пришелец: Неужели? А покажи мне линию.
Вы (осматриваясь по сторонам): Мм… видишь вон тот кирпич? Линия — это один из его торцов.
Пришелец: То есть линия – это часть фигуры?
Вы: Вроде того. Да, большинство фигур состоят из линий. Но линия — это сам по себе базовый концепт: луч света, прямой маршрут на карте, или даже вектор во многих измерениях. Понимаешь?
Пришелец: Линии произошли от кирпичей. Кирпичи, кирпичи, кирпичи…

Видите? Вот потому, что синус постоянно показывают с помощью углов и окружностей, мой мозг думает: «Синус произошел от окружностей. Окружности, окружности, окружности».

Всё, хватит. Вот так будет правильнее: Синус — это естественное колебание, воплощение гладкости: он делает окружности «округлыми» таким же образом, как прямые делают квадраты «квадратами».

Давайте будем строить наше представление о синусе как об отдельной фигуре, и затем поймем, как он встраивается в окружности и так далее. Вперёд!

Синус против прямых

Не забывайте разделять идеи и примеры: квадрат — это лишь пример сочетания линий. А синус как понятие совсем не является «частью окружности».

Давайте рассмотрим синус в симуляторе.

Смайлик начнет свой путь:

• Нажмите start. Давай, смайлик, беги! Заметили это плавное движение вперёд-назад? Этот смайлик и есть синус. В таком же стиле вибрируют струны, сжимаются и разжимаются пружины, вращается маятник… и еще очень много разных тел движутся.
• Измените «vertical» на «linear». Большая разница — видите, какими резкими стали движения на краях амплитуды?

Давайте рассмотрим различия на видео:

• Движение linear постоянно: мы движемся с постоянной скоростью и резко меняем направление. Это неестественное движение, как танцуют в стиле «робот» (на 0:07 движения танцора очень плавные, а на 00:38 он показывает уже стробоскопический эффект).
• Синус меняет свою скорость: начинает двигаться быстро, замедляется, останавливается, а затем снова ускоряется. Ох уж эти очаровательные переходы в танце! (на 0:12 и 0:23 можно увидеть настоящую человеческую синусоиду, а на 00:47 — естественная упругость).

К сожалению, в учебниках танцы не показывают в качестве примера синусоиды. Авторам больше нравится представлять синусоиду изменяющейся во времени (установите «horizontal» в графе «timeline»):

(Википедия)

Проклятие. Вот этот схематический график нам всегда и показывали. Вы по нему представляете, что такое синус? Примерно также, как если бы вас заставили представить ловкость кота по изображению его скелета. Давайте сначала изучим синус в движении, а потом, конечно, изобразим его на графике.

Неизбежная окружность

У окружности есть синус. Да. Но увидеть синус внутри окружности — это всё равно, что получить из омлета яйца обратно, когда все они хорошенько друг с другом перемешаны!

Давайте помедленнее. В симуляторе установите такие параметры: vertical:none и horizontal: sine*. Видите, как смайлик движется вперёд-назад? Это и есть движение синуса. Небольшой фокус: обычно синус начинает свой цикл на нейтральной срединной точке и бежит к максимуму. На этот раз мы начинаем в максимуме и падаем к срединной точке. Синус, который «стартует на максимуме», называется косинусом, и это просто версия синуса (как горизонтальная прямая является версией вертикальной прямой)

Настало время для обеих синусных волн: установите параметры vertical:sine и horizontal:sine*. И… у нас получилась окружность!

Горизонтальные и вертикальные «прыжки» в сумме дали круговое движение. В большинстве учебников рисуют окружность и пытаются извлечь из нее синус, но я предпочитаю обратный подход: начать с простого горизонтального или вертикального движения и добавить противоположное.

Рубрика «Вопросы и ответы»

Первый раз, изучая синусы, я упустил несколько вещей:

Синус вообще-то 1-мерный.

Синус движется в одном измерении. Правда. Мы часто рисуем синус, изменяющийся во времени, а иногда и «предмет», описывающий своим движением синус, тоже куда-то движется, но это уже опционально! Скачок в одном направлении — вполне себе полноценная волна синусоиды.

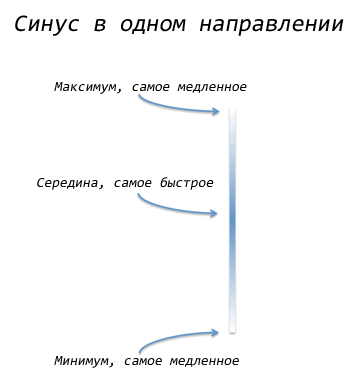
Окружности — это пример синусных волн.

Окружности и квадраты — это комбинации базовых элементов (синусов и прямых отрезков). Но окружности не являются основой синусоиды, как и квадрат не является составной частью прямой.

Что показывают значения синуса?

Синус принимает значения от -1 до 1. Он начинается с 0, возрастает до 1.0 (максимум), падает до -1.0 (минимум) и снова возвращается в нейтральную точку, к нулю. Я также вижу синус как процент от 100% (полный вперёд!) до -100% (полный обратный ход).

Что означает вводное значение ‘x’ в функции sin(x)?

Каверзный вопрос. Поскольку это цикл и х — вводный параметр, он означает, как далеко мы прошли по окружности.

Рассмотрим пример с линиями:

• Мы бродим по квадрату. За 10 секунд мы проходим каждую сторону.
• Спустя 1 секунду, вы прошли 10% от одной стороны
• Спустя 5 секунд, вы прошли одну сторону на 50%
• Через 10 секунд вы пройдете всю сторону.

В линейном движении есть парочка сюрпризов. Рассмотрим теперь синус (сфокусируемся на цикле «от 0 до максимума»):

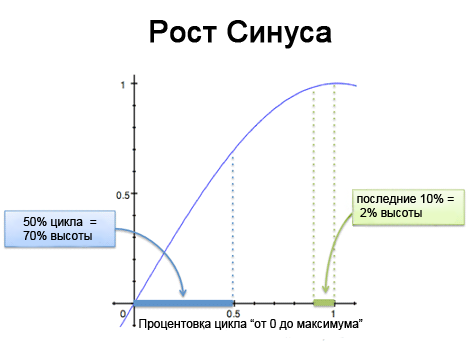
• Мы путешествуем по синусоиде, стартуя с 0 (нейтральная точка) до 1.0 (максимум). И на этот путь у нас ушло 10 секунд.
• Спустя 5 секунд мы…прошли 70%! Синус очень быстрый на старте, и потихоньку замедляется к вершине. Так что большую часть пути мы пройдем за первые 5 секунд.
• И еще 5 секунд нам потребуется на то, чтобы пройти с 70% до 100% пути. А отрезок с 98% до 100% занимает почти целую секунду!

Несмотря на высокую начальную скорость, синус замедляет свой рост, так что мы очень плавно касаемся точки максимума и разворачиваемся назад. Эта плавность и делает синус синусом.

Если вам очень интересны подробности, нажмите «show stats» в симуляторе. Вы увидите процент выполнения полного цикла, мини-цикла (с 0 до 1.0) и текущее значение. Остановите движение (кнопка Stop), попереключайтесь между линейным и синусоидальным движением, чтобы сравнить значения.

Маленькая проверка: Что будет дальше, 10% линейного цикла или 10% синусного? Правильный ответ — синусного.

Помните, в самом начале синус максимально ускорен. Ко времени достижения 50% цикла, синус движется со средней скоростью линейного цикла и, более того, замедляется (пока не достигнет максимума и не развернется).

Так что x — это «количество вашего цикла». Какого цикла?

Зависит от контекста.

• Базовый вариант: ‘x’ — это градусы, и полный цикл состоит из 360 градусов
• Продвинутый вариант: ‘x’ — это радианы (они более натуральные!) и полный цикл составляет полный проход по единичной окружности (2*π радиан)

Поэкспериментируйте со значением х здесь:

Но опять же, циклы зависят от окружностей! Можем ли мы как-то вырваться из-под их тирании?

π без картинок

Представьте себе слепого пришельца, который может различать только тени света и темноты. Можете ли вы объяснить ему, что такое π? Довольно сложно пояснить в такой ситуации понятие длины окружности, верно?

Давайте вернемся немного назад. Синус — это циклическая функция. Это означает, что значит ее значения должны…повторяться! Синус начинается с 0, идет к 1, к 0, к -1, к 0 и так далее.

Давайте определим π как время, за которое синус поднимается с 0 до 1, и обратно возвращается к 0. Вау! Теперь и мы используем π без всяких окружностей!

• Синус — это плавное передвижение вперёд-назад
• π — это время движения синуса с 0 до 1 и обратно до 0
• n * π (0 * π, 1 * π, 2 * π и т.д.) — это момент времени, в котором синус равен 0
• 2 * π, 4 * π, 6 * π и т.д. — полные периоды синуса.

Ага! Вот почему π встречается в таком количестве формул! π не «принадлежит» окружностям больше, чем 0 или 1 — π касается возвращения синуса в центр! Окружность — это пример фигуры, которая повторяется и возвращается в центр каждые 2*π единиц. Но вибрации, скачки и т.д. возвращаются к центру каждый π!

Вопрос: если π — это половина естественного периода, почему оно длится вечно (является иррациональным числом)?

Можно я отвечу вопросом на вопрос, А почему длина диагонали «единичной окружности» равна квадратному корню из 2, который также уходит в бесконечность?

Но да, я понимаю, что это философски не удобно, когда природа ведет себя произвольно. Но что поделаешь…

Насколько быстр синус?

Я вас немного запутал. Сначала я сказал: «представьте, что синусу нужно 10 секунд, чтобы добраться с 0 до максимума». А сейчас я говорю, что ему надо π секунд, чтобы добраться с 0 до максимума и обратно спуститься к 0. Что происходит?

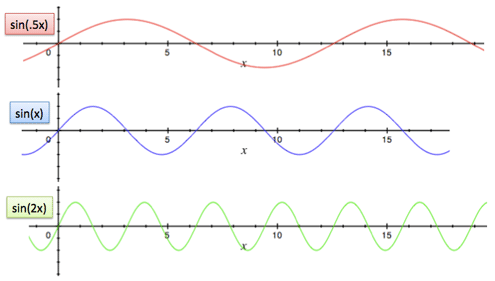
• sin(x) — это базовая синусная волна, которой действительно требуется π единиц времени, чтобы пройти путь с 0 до максимума и опять до 0 (или 2*π, чтобы обойти свой полный период)
• sin(2x) — это синусоида, которая движется вдвое быстрее
• sin(x/2) — это синусоида, которая движется вдвое медленее базовой

Так что мы используем sin(n*x) , чтобы сделать синус, который будет двигаться так быстро, как нам нужно. Очень часто слово «синусоида» используется для указания общей формы волны, а не конкретной скорости.

Часть 2: Понимание определений синуса

Это сложно — так что сделайте перерыв, наберитесь сил. Надеюсь, скоро в нашем сознании вырисуется синус как отдельное понятие. Давайте найдем связь между привычными определениями синуса.

Определение 1: Высота треугольника / окружности!

Синус впервые нашли в треугольнике.

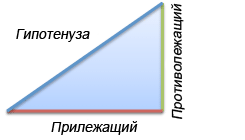
• Синус — это отношение противоположного катета к гипотенузе
• Косинус — это отношение прилежащего катета к гипотенузе
• Тангенс — это соотношение между противоположным и прилежащим катетами

Для прямоугольного треугольника с углом х, sin(x) — это длина противолежащего катета, поделенная на длину гипотенузы. Если мы возьмем гипотенузу, равную 1, то это определение можно упростить до:

• Синус = Противолежащий катет
• Косинус = Прилежащий катет

А с большим умом, мы можем нарисовать треугольник с гипотенузой 1 в окружности с радиусом 1:

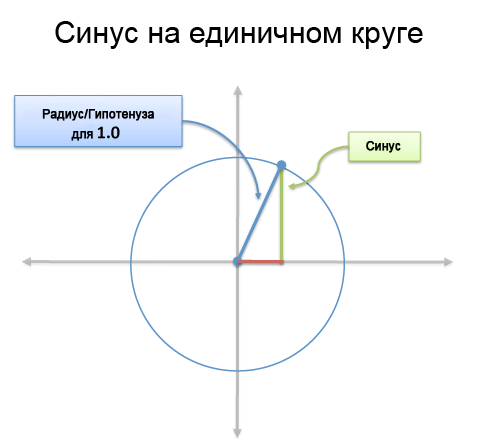
Вуаля! Окружность, содержащая все возможные прямоугольные треугольники (поскольку размер треугольника из единичной окружности можно масштабировать до любого размера). Например:

• sin(45) = 0.707
• Возьмите 10-метровый столб и поднимите его с земли на 45 градусов. Верхушка столба будет 10 * sin(45) = 7.07 метров от земли
• А 8-метровый столб будет 8 * sin(45) = 5.65 метров от земли

Подобные манипуляции со столбами очень полезны в строительстве (пирамиды сами себя не рассчитают). К сожалению, спустя тысячи лет у нас твердо закрепилась мысль, что смысл синуса в возможности вычислить высоту треугольника по гипотенузе и углу. Нет и еще раз нет, синус — это форма, которую можно обнаружить в окружностях (и треугольниках). В реальности, мы часто переходим в «режим геометрии» и для краткости мыслительного процесса думаем «синус=высота». Это нормально, главное не застревать на этом, а смотреть шире.

Определение 2: Бесконечный ряд

Я спрятал слона в комнате: как мы вообще вычисляем синус? Мой калькулятор, что, каждый раз рисует окружность и замеряет его?

Рад вам поведать, как можно вычислить синус без окружностей.

Синус — это ускорение в сторону, противоположную тому, где вы находитесь.

Пользуясь нашим примером с банковским счётом: представьте, что ваш шеф каждую неделю решил менять вашу зарплату на сумму, противоположную текущей на вашем банковском счёте. Если у вас сейчас есть 50 рублей, на следующей неделе шеф выдаст на 50 рублей меньше. Конечно, поскольку ваш доход будет 75 рублей, вы всё еще будете в плюсе (75 — 50) но в итоге ваш баланс уменьшится, поскольку «прибавки» шефа превзойдут ваши доходы.

Но не отчаивайтесь! Как только баланс становится отрицательным (скажем, у вас -50 рублей), ваш босс выдаст вам на целых 50 рублей больше. Затем снова баланс станет отрицательным (с его ростом шеф выдает всё меньше денег), и так будет продолжаться постоянно. Баланс будет то положительный, то нулевой, то отрицательный.

Этот пример также поясняет, почему в нейтральной точке (в 0) скорость синуса максимальна: когда вы на максимуме, вы начинаете падать и собирать всё больше «отрицательных прибавок», которые довольно быстро тянут вас к 0. После прохождения 0 вы начинаете получать наиболее значительные положительные прибавки и замедляетесь., потому что как только уходите в плюс, шеф опять начинает отнимать от вашей зарплаты.

Между прочим: поскольку синус — это ускорение, обратное к вашему текущему положению, а окружность сделана из горизонтальной и вертикальной синусоиды… вы поняли! Круговое движение может быть описано как «постоянное движение в направлении, противоположном текущей позиции, по направлению к горизонтальному и вертикальному центру».

Покопаемся в расчётах

Давайте опишем синус с помощью вычислений. Как в случае с e, мы можем разбить синус на маленькие части:

• Начнем с 0 и дорастем до единичной скорости
• В каждый момент времени мы будем замедляться из-за отрицательного ускорения

И как обо всем этом думать? Посмотрите, как каждое наше действие изменяет расстояние от центра:

• Наш первый скачок увеличивает расстояние линейно: у (расстояние от центра) = х (затраченное время)
• В любой момент, мы чувствуем возвращающую силу -х. Мы интегрируем дважды, чтобы обратить отрицательное ускорение в расстояние:
  

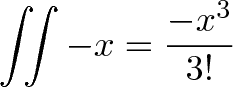
Понимание того, как ускорение влияет на расстояние, похоже на наблюдение за тем, как прибавки влияют на ваш банковский счёт. «Прибавка» должна изменять ваш доход, а ваш доход изменяет состояние вашего банковского счёта (два интеграла «по команде»).

Так что после «х» секунд, мы уже догадаемся, что синус это «х» (начальный импульс) минус x^3/3! (эффект ускорения):

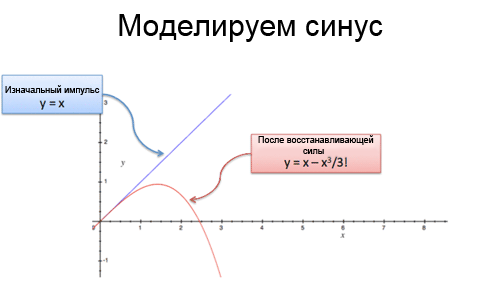
Что-то не так — синус не спадает! В случае с е мы видели, что «проценты приносят свои проценты», в случае с синусом происходит то же самое. «Возвращающая сила» меняет наше расстояние на -x^3/3!, что создает другую возвращающую силу. Рассмотрите пружину: если отпустить пружину с грузиком внизу, то толчок будет достаточно большим, чтобы создать другой толчок, который потянет грузик обратно вверх, а потом снова вниз. Ох уж эти неугомонные пружины!

Нам нужно рассмотреть каждую возвращающую силу:

• y = x — это наше изначальное движение, которое создает возвращающую силу удара:
• y = -x^3/3!, которая создает возвращающую силу удара:
• y = x^5/5!, которая создает возвращающую силу удара:
• y = -x^7/7!, которая создает возвращающую силу удара…

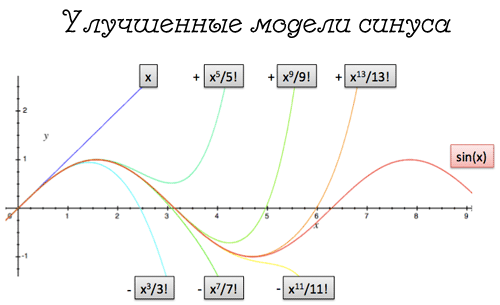
Точь-в-точь как е, синус можно описать бесконечным уравнением:

Я видел эту формулу много раз, но до меня дошел ее смысл только когда я представил синус как комбинацию начального импульса и возвращающих сил. Начальный импульс (y = x, растет вверх) в итоге превосходит возвращающая сила (которая толкает нас вниз), и эта сила в свою очередь постепенно компенсируется своей возвращающей силой (что снова толкает нас вверх), и так далее.

Пара интересных заметок:

• Рассматривайте «возвращающую силу» как «положительный или отрицательный процент». Так проще понять связь синуса и е в формуле Эйлера. Синус ведет себя как е, кроме моментов, когда он начинает зарабатывать отрицательный процент. Тут нам еще надо поучиться :).
• Для маленьких чисел «y = x» — неплохое предположение для синуса. Мы просто берем начальный импульс и игнорируем возвращающие силы.

Вычисление косинуса

Косинус — это просто смещенный синус, и очень хорошо, что теперь нам с синусом всё ясно:

• Синус: начинается с 0, начальный импульс y = x (100%)
• Косинус: начинается с 1, никакого начального импульса нет

Косинус просто начинает…сидит на 1. Мы запускаем в работу возвращающую силу:

Опять же, мы интегрируем —1 дважды, чтобы получить -x^2/2!. Но это провоцирует другую возвращающую силу, и вот что в итоге получается:

Определение 3: Дифференциальное уравнение

Мы описали поведение синуса определенными уравнениями. Вкратце это будет выглядеть так:

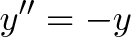
Эта красота означает следующее:

• Наша текущая позиция — y

• Наше ускорение (2-я производная, или у”) — обратно нашей текущей позиции (-y)

Это справедливо и для синуса, и для косинуса. Сначала я просто ненавидел это определение; оно такое непохожее на нашу визуализацию. Я не понимал, что оно описывало суть синуса: «ускорение, обратное текущей позиции».

И вспомните как синус и е связаны? Ну, e^x можно описать уравнением:

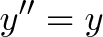
То же уравнение с положительным знаком («ускорение равно текущей позиции»)! Когда синус — это «высота окружности», очень тяжело проследить связь с е.

Одним из моих серьезнейших математических сожалений является то, что я еще не изучил дифференциальные уравнения. Но я хочу это сделать, и подозреваю, что правильное понимание синуса и экспоненты сыграют в этом решающую роль.

Подытожим

Моей целью было отделить синус от тривиальных математических определений («часть окружности») и придать ему свою собственную форму:

• Синус — это плавное, колебательное движение между минимумом (-1) и максимумом (1). Математически вы ускоряетесь обратно направлению своего движения. Этот «отрицательный процент» удерживает синус от бесконечного роста.
• Синус встречается в окружностях и треугольниках (а также вибрациях, звуковых волнах, колебаниях маятника и т.д.).
• π — это время, за которое sin(x) проходит от 0 до 0. Он не «принадлежит» окружностям больше, чем 0 или 1.

Синус станет одним их ваших умственных инструментов (Хм, мне нужна формула для описания плавных изменений…).

В итоге мы поймем основы интуитивно (е, π, радианы, мнимые числа, синус…) и научимся смешивать их в великолепный математический салат. Приятного аппетита!

Перевод статьи «Intuitive Understanding of Sine Waves»