В высшей математике и матанализе все примеры — скучные. "Эй, ребятки! Вы когда-нибудь вообще интересовались расстоянием, скоростью и ускорением движущейся частицы? Нет? Ну, этим мы будем заниматься весь урок!"
Я люблю физику, но это не самый лучший способ разобраться. Мы обречены ждать того момента, когда начнутся лабораторные занятия, или хуже того, это превращает матанализ в "математику для лабораторных занятий". Нельзя ли объяснить это на вещах попонятнее, и желательно применить к реальной жизни?
Думаю, вполне можно. Итак, вот наша цель:
- использовать деньги, а не физику, чтобы разобраться с принципами матанализа,
- посмотреть, как соотносятся разные понятия: банковский счёт и зарплата, затем зарплата и надбавка,
- посмотрим, что ещё можно из этого выжать — можно ли исследовать глубже.
Надейвайте ваши матановые шлемы — время погружаться.
Деньги, денежки, деньжищи
Мой любимый пример из матанализа — это отношение накопительного банковского счёта, зарплаты и надбавки к зарплате.
Знакомьтесь, это Джо ("Привет, Джо!"). Вы, пронырливый мерзавец, проникаете в компьютер Джо и отслеживаете движение по его банковскому счёту каждую неделю. Что полезного вы можете из этого выудить?
 Оп-па! Вообще-то, нечего тут ловить — Джо ничего не получает. А что, если вы теперь видите такую картинку?
Оп-па! Вообще-то, нечего тут ловить — Джо ничего не получает. А что, если вы теперь видите такую картинку?
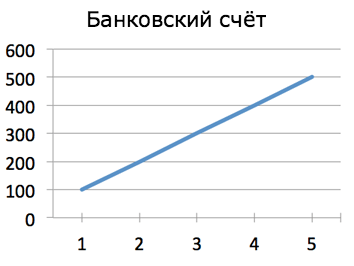
Тут всё просто: Джо, похоже, зашибает деньгу. Но сколько? Быстренько посчитав в уме разницу, мы можем определить, сколько ему платят в неделю. Ясно, что Джо получает 100 монет каждую неделю.
- Ключевая мысль: если я знаю, как быстро растёт твой счёт в банке, я знаю твою зарплату.
Сумма на счету в банке зависит от зарплаты — эта сумма изменяется из-за еженедельных выплат.
Кому надбавки?
Идём дальше: что ещё мы можем разведать, имея данные о зарплате? Вообще-то, зарплата тоже поддаётся анализу — мы можем проследить, изменяется ли она! Стало быть, мы можем определить, меняется ли зарплата Джо от недели к недели (получает ли он надбавку?).
План таков:
- взять понедельную разбивку банковского счёта Джо,
- посчитать разницу по счёту и получить данные по его зарплате,
- посчитать разницу по зарплате и получить данные по надбавке (если таковая имеется).
В первом примере (100 монет в неделю) очевидно, что никакой надбавкой там и не пахнет (прости, Джо). Основная идея в том, чтобы "найти разницу" и проанализировать первое соотношение (счёта и зарплаты), и потом "найти разницу ещё раз", чтобы проанализировать второе соотношение (зарплаты к надбавке).
Отматываем назад
Мы сейчас двигались в одном направлении — от банковского счёта к зарплате. А работает ли это в другую сторону — если я знаю зарплату, могу ли я предсказать, сколько осядет на счету в банке?
Я вижу, вы медлите с ответом. Да, знать, что Джо получает 100 монет в неделю — неимоверно здорово. Однако... не нужно ли нам учесть то, сколько было на счету изначально?
Чертовски верно! Просто цифры прироста по счёту или зарплате явно недостаточно — с какой отметки начинать-то? Для упрощения (например, в домашней работе) часто допускают, что Джо начал с нуля. Но раз уж вы делаете предположение, вам наверняка хотелось бы знать изначальные условия (то самое преславутое "+ С" в формуле первообразной).
Пример посложнее
Допустим, накопительный счёт Джо растёт вот так: 100, 300, 600, 1000, 1500...
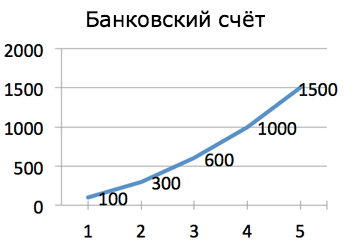
Так, что мы тут видим? Случайный набор цифр? Давайте высчитаем разницу по неделям, и получим такую картину:
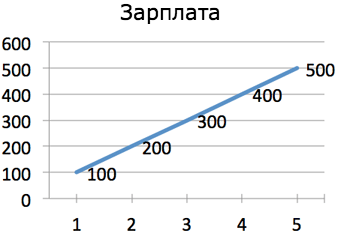
Любопытненько — зарплата Джо возрастает каждую неделю! Давайте ещё раз найдём разницу по неделям и посмотрим, что получится:
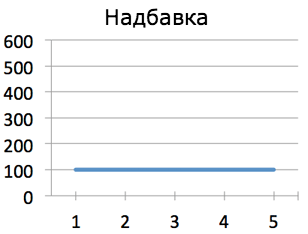
И вуаля — оказывается, Джо получает регулярное повышение зарплаты на 100 монет в неделю. Не будем останавливаться на достигнутом — давайте нанесём это всё на единую шкалу:
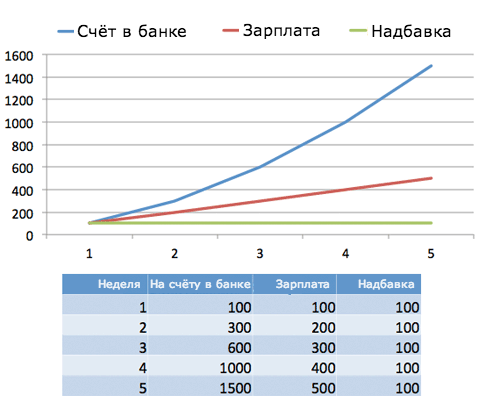
Тут можно рассуждать так: Джо получает повышение зарплаты каждую неделю, из-за этого растёт зарплата, из-за чего увеличивается счёт в банке. Пока надбавка растёт, растёт и зарплата, что также сильно влияет на накопительный счёт. Можно представить себе, что надбавка "раздувает" зарплату, а из-за раздувающейся зарплаты, в свою очередь, "набухает" и банковский счёт.
Ну и... где тут матанализ?
Как выглядит формула для нахождения состояния счёта в банке нашего Джо для любой заданной недели? Ну, это сумма всех его зарплат до этого дня:
100 + 200 + 300 + 400... = 100 × n × (n + 1)/2
Формула суммы последовательности чисел (1 + 2 + 3 + 4...) близка к n2/2, и приближается к ней по мере роста числа слагаемых.
Итак, вот наши первые результаты по математическому анализу:
- постоянная надбавка (100 монет/неделю) приводит к тому что, ...
- ...линейно растёт зарплата (100, 200, 300, 400), что ведёт к...
- ...квадратичному (что-либо × n2) возрастанию счёта в банке (100, 300, 600, 1000... ну вы видели кривую!)
А почему там приблизительно ½ × n2, а не просто n2? Дам подсказку: линейное возрастание зарплаты (100, 200, 300) даёт нам треугольник. Площадь этого треугольника представляет собой сумму всех выплат, а площадь прямоугольного треугольника равняется ½ × основание × высота. Основание равняется n — числу недель, а высота (прибыль) есть 100 × n.
Такие геометрические манипуляции становятся сущим адом при работе с более сложными задачами — тот факт, что мы можем посчитать 2 × 100 с хвостиком, не означает, что это лучший путь. Матанализ предоставляет нам более мощный инструментарий (производные и интегралы).
Разбираемся с деталями
Наше понимание общей картины с банковским счётом, зарплатой и надбавкой позволяет нам заглянуть глубже.
А можно подсчитать общий доход от 1 недели до 10?
Конечно! Есть два варианта: можно поочерёдно сложить доход за каждую неделю (зарплата за первую неделю + зарплата за вторую неделю + ...), либо же посчитать разницу на счету: сумма по счёту на 10 неделе минус сумма по счёту на первой неделе. У этого метода есть крутое название: Фундаментальная Теорема Матанализа!
Можно ли пойти дальше и найти производную для надбавки?
Ну почему нет? Допустим, надбавка составляет 100 монет/неделю; если мы возьмём производную, то увидим, что она упала до 0 (ведь нет "надбавки для надбавки", она остаётся на неизменном уровне). Однако же, мы вполне можем представить себе ситуацию, когда надбавка тоже возрастает (надбавка первой недели = 100, надбавка второй недели = 200, и т.д.). Пользуясь нашими идеями: если "надбавка надбавки" постоянная, сама надбавка будет расти линейно (что-то × n), зарплата изменяется квадратично (что-то × n2), а счёт в банке растёт кубически (что-то × n3). Ну и в общем-то всё сходится!
Могут ли производные находиться бесконечно?
Ага. Кто знает, может наша последовательность выглядит так: банковский счёт → зарплата → надбавка → инфляция → надой коровы фермера Джо → качество кормёжки коровы фермера Джо. Многие схемы "перестают давать производные", как только мы добираемся до корня проблемы. Но некоторые интересные ситуации, вроде экпоненциального роста, имеют бесконечное число производных! Вы получаете доход, который приносит доход, который приносит доход, ... бесконечно! В таком случае, вы никогда не докапаетесь до исходной причины роста вашего банковского счёта, потому что на него влияет бесконечно число факторов (всё довольно хитро).
А что будет, если производная стала отрицательной?
Хороший вопрос. Если надбавка станет отрицательной, зарплата начнёт уменьшаться. Однако, до тех пор, пока зарплата выше нуля, счёт в банке будет расти! Посудите сами: 100 монет зарплаты вместо 200, конечно, вас не сильно обрадуют, но всё ещё увеличивают ваши накопления в банке. В конце концов, отрицательная надбавка (в таком случае, штраф) пересилит зарплату, и та станет отрицательной, что означает, что теперь Джо платит своему начальнику. Но до тех пор счёт в банке будет увеличиваться.
Как быстро можно находиться производные?
Представьте, что мы анализируем портфель акций, а не банковский счёт. В таком случае, нам понадобилось бы строить нашу модель с зарплатой и счётом на посекундных данных. Идея в том, чтобы использовать настолько короткие интервалы, насколько нам нужно — достаточно серьёзную часть матанализа занимает раздел, который позволяет сказать, "вот такой предел — достаточно точный для меня".
Формулы математического анализа, которые вам обычно попадаются (интеграл от x = 1/2 × x2) отличаются от "дискретных" (сумма от 1 до n = 1/2 × n × (n+1)), потому что в случае дискретных подсчётов используются "кусочные" интервалы.
Что мы имеем в итоге
Зачем мы заморачивались с такой аналогией? Затем, что привычные "расстояние, скорость, ускорение" не приводят к правильным вопросам. Вот какая следующая производная от ускорения?.. (Она называется "толчок" и довольно редко используется). Такой узколобый пример похож на то, как если бы дети думали, что умножение нужно исключительно для нахождения площади, и вообще работает только для двух чисел за раз.
Вот ключевые моменты:
- математический анализ помогает нам находить взаимосвязи (банковский счёт с зарплатой и затем с надбавкой),
- производная "стремится вниз" (можно посчитать разницу неделю за неделей и отыскать значение зарплаты),
- интеграл "стремится вверх" (складываем зарплаты — получаем банковский счёт),
- мы можем найти формулу для нужной задачи (имея данные по счёту, предсказать зарплату) или найти нужное значение (какова моя зарплата на третью неделю?),
- матанализ полезен и помимо супер-сложных научных вопросов. Если у вас есть данные или формула (уровень производительности, размер населения, ВВП страны) и вы хотите исследовать их поведение, математический анализ — ваш инструмент,
- матанализ по учебнику предполагает запоминание правил дифференцирования и интегрирования. Запомни основы (xn, e, ln, sin, cos) и остальное предоставь компьютерам. Наш мозг лучше приспособлен к тому, чтобы переводить наши мысли на язык математики.
В мире моей мечты производная и интеграл станут обыденными вещами. Ведь они являются тем, что можно делать с формулами — так же, как вычитание и сложение являются тем, что можно делать с числами.
"Ребятушки, мы находим общую массу с помощью суммы (масса1 + масса2 = масса3). А чтобы найти, как изменится наше местоположение, мы используем производную."
"Ну да, сложение позволяет совмещать вещи. И да, надо найти производную, чтобы узнать, как меняется положение. Как бы ты считал это по-другому?"
Всегда приятно помечтать. Приятных вычислений!
Перевод статьи "Understanding Calculus With A Bank Account Metaphor".

