Я изучал теорию вероятности и статистику без практики, поэтому у меня не было чёткого понимания, в чем же разница между ними? Для чего обе эти науки?
Мне помогла такая аналогия:
- Вероятность — это когда стоишь рядом с каким-то зверем и гадаешь, какой же след оставят его лапы на земле.
- Статистика — это когда видишь след, и угадываешь, какое животное его оставило.
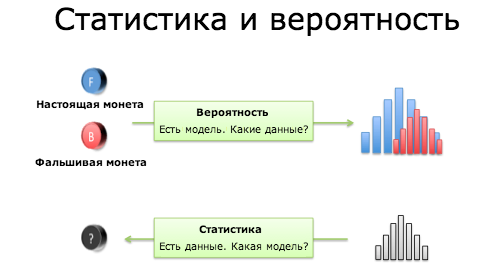
Вероятность довольно проста: у вас есть медведь. Измерьте ширину и длину его лапы, и вы уже можете представить его следы на земле. “Миша весит 200 кг, и длина его конечностей 90 см, он оставит вот такой след”. Приведу более привычный науке пример: “У нас есть симметричная монета. После 10 подбрасываний возможны такие исходы”.
Со статистикой все сложнее. Мы замеряем отпечатки лап, и по полученным данным должны вычислить, какой зверь их оставил. Медведь? Человек? Если у нас 6 раз монета выпала орлом и 4 — решкой, какие шансы того, что монета симметрична, то есть вероятность выпадения орла и решки одинакова?
Ищем подозреваемых
Вот как мы “вычислим животное” с помощью статистики:
Получите следы. Каждый кусочек данных — это точка в общей картине. Чем больше данных, тем чётче форма следа (согласитесь, имея бесформенную кляксу вместо чёткого отпечатка лапы сложно будет определить тенденцию).
Измерьте базовые характеристики. Каждый отпечаток имеет глубину, ширину и высоту. Каждый массив данных имеет среднее значение, медиану, среднеквадратическое отклонение и т.д. Эти общие описания отпечатков дают грубое приближение: “Отпечаток имеет размер всего 15 см в ширину: кто же это — маленький медведь или большой человек?”
Отыщите виды. Существуют десятки потенциальных владельцев следов (распределение вероятностей), которые можно рассмотреть. Мы сужаем этот выбор полученными знаниями о системе. След находится в лесу? Это, возможно, лошади, но точно не зебры. Лучше задавать вопросы, на которые можно ответить только “да” и “нет”, рассматривая биномиальное распределение.
Ищите конкретное животное. Как только мы определились с распределением (“медведи”), мы сверяем наши полученные данные с табличными. “След 15 см в ширину, 5 см в глубину наиболее похож на след 3-летнего, 200-килограммового медведя”. Справочная таблица генерируется, исходя из распределения вероятностей, то есть на основе замеров настоящих животных.
Выдвигайте дополнительные предположения. Как только мы знаем, что за животное оставило следы, мы можем предугадать его поведение в будущем и другие характерные черты ("Согласно нашим расчетам, в лесу Миша проголодается"). Статистика помогает нам узнать об источнике данных, исходя из самих данных.
Да, метафора не идеальна, но куда более приятная, чем “Статистика — это наука о сборе, структурировании, анализе и интерпретации данных”. Нужны доказательства? Давайте пройдем небольшой тест, ответьте на эти вопросы:
- Какие самые распространенные виды животных? (распределения вероятностей)
- Были ли открыты новые виды?
- Можем ли мы предугадать, каким будет следующий отпечаток? (Экстраполяция)
- Следуют ли отпечатки определенному пути (Регрессия / линия тренда)
- Есть два следа, какое из животных быстрее? Больше? (данные из клинических испытаний двух лекарство: какое показало себя более эффективным?)
- Движется ли второй зверь в одном направлении с первым? (Корреляция)
- Идут ли оба зверя по одному и тому же следу? (Причинная зависимость: оба медведя преследуют одного зайца)
Эти вопросы куда более глубоки, чем те, о которых я размышлял, изучая статистику впервые. Каждая мелкая процедура приобретает смысл: мы изучаем новые виды? Как снять замеры с отпечатка? Как составить таблицу из распределения вероятностей? Как отыскать размеры в таблице?
Такая аналогия со статистикой делает дальнейший анализ данных куда проще. Приятных вычислений.
P.S. В математике существует множество противоположных понятий, таких как вероятность и статистика. Некоторые действия очень легко выполнить (производные), но сложно вернуться на шаг назад (интегралы).
Перевод статьи «A Brief Introduction to Probability & Statistics»

