Пытаясь понять теорему Байеса, я решил, что сначала надо собрать сведения, а затем найти закономерность в появлении ложных результатов. Означает ли положительный результат анализа, что вы больны? Ну, вроде того, насколько редко встречается то или иное заболевание, и как часто здоровые люди получают положительный результат по анализу? Все эти обманчивые явления нужно тщательно рассмотреть.
Этот подход помог мне кое-как преодолеть практические проблемы, но я всё равно не мог думать как Байес. На моем пути появились большие препятствия:
С процентами очень трудно договориться. Коэффициенты сравнивают относительную частоту сценариев (А:В), в то время как проценты отражают отношение частоты конкретного сценария к их общему количеству [A/(A+B)]. У монетки равные шансы (1:1), т.е. вероятность выпадения каждой из сторон 50%. Отлично. А что случится, если сторон у монетки будет 18? Ну, тогда шансы выпадения одной из них будут 18:1. Сможете быстренько выдать десятичный процент вероятности? (Я подожду…). Очевидно, что с коэффициентами требуется гораздо меньше вычислений, так что давайте с них и начнем.
Уравнения старательно скрывают смысл самой теоремы. Вот теорема Байеса в ее обычном представлении:
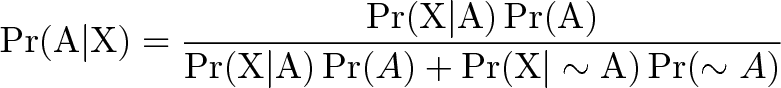
Теорема читается справа налево, с кучей условных вероятностей. А как вам такая версия:
оригинальные коэффициенты * поправка результата = новые коэффициенты
Байес начинал с предположения (коэффициент 1:3 на то, что будет дождливо : солнечно), брал очевидные факты (сейчас июль-месяц, мы в Сахаре, вероятность солнечной погоды в 1000х раз выше дождя), и обновлял свое предположение (шансы 1:3000, что будет дождь : солнечно). “Поправка результата” отражает, насколько лучше, или хуже, стал наш коэффициент с учётом дополнительной информации (если бы это был сентябрь в Питере, то можно было бы утверждать, что дождь в 1000х раз вероятнее солнца).
Давайте попробуем поработать с процентами, после чего плавно перейдем к комплексной версии.
Специалист по статистике эпохи каменного века
Нашего пещерного человека зовут Ог, и он только что провел статистическое исследование для своего племени. Вот его результаты:
- Он увидел 50 оленей и 5 медведей (вероятность 50:5)
- Вечером он увидел 10 оленей и 4 медведя (вероятность 10:4)
Какие выводы из этого можно сделать? Вот:
исходные вероятности * поправка результата = новые вероятности
или
поправка результата = новые вероятности / исходные вероятности
Вечером он осознал, что олень стал на 1/4 более вероятным, чем до этого:
10:4 / 50:5 = 2.5 / 10 = 1/4
(Попробуйте с другой стороны, вечером медведи стали в 4 раза вероятнее)
Давайте немного проясним коэффициенты. А:В описывает, сколько А мы получим на каждый В (представьте количество километров на литр топлива, как км : л). Сравните значения делением: переход от 25:1 до 50:1 означает, что вы удвоили эффективность (50/25 = 2). Точно также, мы только что вычислили, как менялось отношение "оленей к медведям".
Ог радостно продолжает излагать результаты:
- У реки появление медведей в 20х раз более вероятно (он видел 2 оленя и 4 медведя, то есть 2:4 / 50:5 = 1:20).
- Зимой оленя можно увидеть в 3 раза чаще (30 оленей и 1 медведь, 30:1 / 50:5 = 3:1).
Он берет сценарий, сравнивает его с базовым вариантом, и вычисляет поправку результата.
Другой пещерный человек, назовем его Бо, подписался на журнал Ога, и хочет добавить к исследованию данные по своему лесу (где олени : медведи имеют коэффициент 25:1). Вот что Бо вычислил:
- Его общая оценка составляет 25:1 для оленей : медведей
- Вечером олени в 4х раз вероятнее => 25:4
- У реки медведи являются чаще в 20х раз => 25:80
- А зимой олени в 3х раз чаще => 75:80
В результате Бо получает, что вероятность увидеть медведя почти такая же, как вероятность увидеть оленя.
Он пришел к этому путем Байеса:
- начал с предварительной вероятности, общего коэффициента еще до своих собственных наблюдений
- собрал сведения для своей местности и определил, как сильно они изменят первоначальные коэффициенты
- Вычислил апостериорную вероятность и коэффициенты после обновления информации.
Байесовский спам-фильтр
Давайте сделаем спам-фильтр на основе Байесовского детектора медведей Ога.
Для начала соберем коллекцию обычных писем со спамом. Запишем, как часто каждое слово появляется в этих письмах:
спам не спам
привет 3 3
дорогой 1 5
купить 3 2
виагра 3 0
...
(“привет” появляется одинаковое количество раз в спаме и не-спаме, а вот “купить” чаще можно встретить именно в спаме)
Мы вычисляем коэффициенты точно также, как делали при анализе оленей : медведей. Давайте предположим, что входящее письмо является спамом с вероятностью 9:1, и в нашем письме встречается “привет дорогой”:
- Произвольное письмо имеет шансы быть спамом 9:1
- Поправка для слова “привет” => коэффициент остается прежним — 9:1 (“привет” встречается одинаково часто в обоих случаях)
- Поправка для слова “дорогой” => шансы 9:5 (“дорогой” появляется в 5x раз чаще в спаме, чем в нормальном письме)
- Вероятность спама с “привет дорогой” => 9:5
Получается, что спам с таким текстом имеет вероятность 9:5. Но согласитесь, эта вероятность меньше, чем начальный показатель (9:1).
А теперь рассмотрим сообщение с “виагра купить”:
- Начальный коэффициент спама 9:1
- Поправка для “купить”: 27:2 (3:2 шансы встретить слово в спаме)
- Поправка для “виагра” …придется делить на ноль!
“Виагра” еще ни разу не встречалась в нормальном письме. Это гарантия того, что письмо — спам?
Возможно, и нет: нужно быть готовым к разным случаям. Давайте представим, что есть нормальное письмо, в котором где-то встретилось слово “виагра”, и вероятность такого явления 3:1. Наши шансы становятся 27:2 * 3:1 = 81:2.
Это уже что-то! Изначальная вероятность 9:1 изменяется на 81:2. Является ли это письмо спамом?
Насколько вероятен ложный результат?
Вероятность 81:2 подразумевает, что на каждые 81 письмо с такими словами мы заблокируем 2 нормальных письма, посчитав их за спам. Этот коэффициент слишком большой. Если проанализировать данные более детально (взять для анализа больше слов или включить другие характеристики), мы, скорее всего, придем к коэффициенту 1000:1 отнесения сообщения к спаму.
Открытие теоремы Байеса
Мы можем проверить нашу интуицию, задавая правильные вопросы:
- Действительно ли анализируемые факты независимые? Есть ли какая-то связь между поведением животных вечером и зимой, или между словами, которые встречаются в одном письме? Конечно. Мы “наивно” принимаем сведения за независимые факты (но даже так мы умудряемся создавать довольно эффективные спам-фильтры).
- Сколько нужно данных для анализа? Если мы увидели 2 оленя и 1 медведя, будет ли выведенная вероятность 2:1 справедливой и для большего числа зверей, скажем, 200 оленей и 100 медведей?
- Насколько точными была начальные коэффициенты? Исходные убеждения меняют всё. (“Байес — это тот, кто, ожидая лошадь, мельком завидев ослика, твердо будет уверен в том, что увидел мула”). (Мул — гибрид лошади и осла).
- Играют ли абсолютные вероятности какую-то роль? Обычно нам нужна наиболее вероятная теория (“Олень или медведь?”), а не глобальная вероятность сценария (“Каковы шансы появления оленей вечером зимой у реки против появления медведей вечером зимой у реки?”). Многие Байесовские расчёты игнорируют глобальные вероятности, которые сокращаются при делении, и опираются на частный подход.
- Можно ли обмануть наш фильтр? Спам может содержать куски нормального текста, чтобы выдать себя за нормальное письмо и обмануть фильтр. Вы и сами не раз замечали такие письма, которые по ошибке были приняты за спам.
- Какие данные мы должны использовать? Дайте информации говорить за себя. У имейлов может быть масса характеристик (время, заголовки, страна, HTML-теги). Присвойте каждой характеристике коэффициент вероятности, и дайте Байесу их проанализировать.
Мыслите пропорциями и процентами
Пропорциональный и процентный подходы отвечают на разные вопросы:
Пропорции: Даны вероятности каждого исхода, как они изменятся с учётом анализа наблюдений?
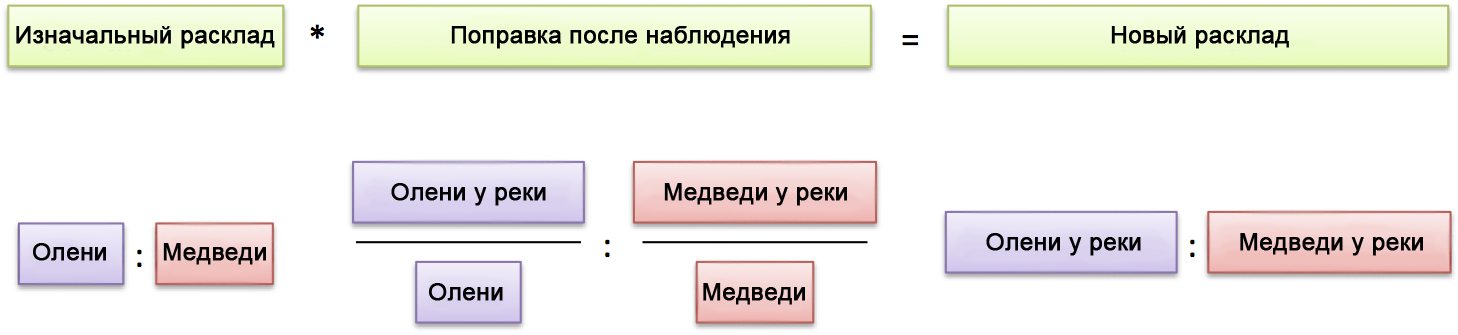
Поправки результата просто искажают начальные вероятности.
Проценты: Каков шанс исхода после получения подтверждающих данных?
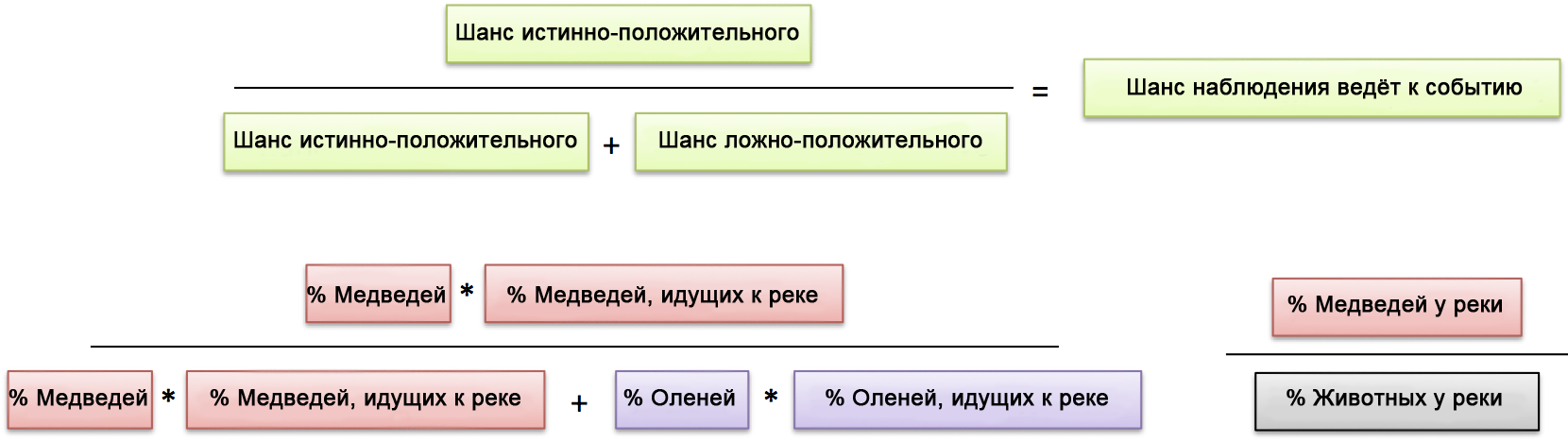
В случае процентов,
- “% медведей” — это общие шансы встретить медведя где-либо
- “% медведей, идущих к реке” — насколько вероятно, что медведь достигнет реки.
- “% медведей у реки” — это комбинированная вероятность (медведь шел к реке, и дошел). Языком статистики, получается
P(событие и подтверждение) = P(событие) * P(подтвержденное событие) = P(событие) * P(подтверждение|событие)
Давайте рассмотрим пример из медицины: количество больных раком
- 1% населения больно раком
- 9.6% здоровых людей получают положительный результат анализа, как и 80% людей, больных раком.
Если вы видите положительный результат, каков шанс, что в организме действительно развивается рак?
Пропорциональный подход:
- Рак: шансы быть здоровым 1:99
- Поправка в соответствии с реальными данными: 80/100 : 9.6/100 = 80:9.6 (80% больных имеют позитивный тест, как и 9.6% больных).
- Конечная пропорция: 1:99 * 80:9.6 = 80:950.4 (шансы иметь рак при положительном тесте примерно 1:12, ~7.7%).
Даже при росте в 8.3х раз (80:9.6) вероятности при положительном тесте, рак остается довольно маловероятным.
Процентный подход:
- Шансы иметь рак — 1%
- Шансы правдивого положительного результата = 1% * 80% = 0.008
- Шансы ложноположительного результата = 99% * 9.6% = 0.09504
- Шансы иметь рак = 0.008 / (0.008 + 0.09504) = 7.7%
Написав показатель в виде процентов, мы перешли к абсолютным шансам. Глобальный шанс найти больного пациента с положительным результатом — 0.8%, а глобальный шанс найти здорового пациента с положительным результатом — 9.504%.
Лучше, когда оба эти подхода дополняют друг друга: проценты используются для быстрого результата, а пропорции — для отслеживания изменений вероятностей каждого исхода. Оставим мириады интерпретаций теоремы Байеса на другой раз.
Приятных вычислений!
Перевод статьи «Understanding Bayes Theorem With Ratios»

