Свободный полет по производным

Каким способом лучше всего объяснить понятие производной? Вот моя версия.

Производная — это сердце вычислений, похороненное внутри этого определения:

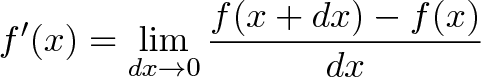
Но что оно на самом деле значит?

Представим, что я дал вам волшебную газету, в которой приведены ежедневные изменения на фондовом рынке на следующие несколько лет (+1% на понедельник, -2% на вторник и т.д.). Что бы вы могли с ней делать?

В принципе, производя эти изменения по одному, вы бы могли узнать будущие цены и покупать дешевле / продавать дороже разные валютные пары, чтобы баснословно разбогатеть.

Также производную называют “наклоном функции” — как же это упрощённо! Производная — это полное понимание поведение системы, позволяющее предсказывать её будущее. Вы можете графически представить прошлое, настоящее и будущее, вычислить минимумы и максимумы, и многое-многое другое.

Давайте отступим от того грубого уравнения. Уравнения существуют, чтобы передавать идею, нам же нужно её понять, а не копаться в грамматике.

Производные создают идеальную модель изменения из неидеального предположения.

Эта мысль — результат тысячелетних раздумий, от Архимеда до Ньютона. Давайте посмотрим, что за ней стоит.

Мы все живем в сияющей бесконечности

Бесконечность — это постоянный источник парадоксов (“головных болей”):

• Прямая состоит из точек? Конечно.
• И в ней бесконечное количество точек? Ага.
• Как вообще можно пройтись по комнате, встречая бесконечное количество точек на своем пути? (ох уж этот парадокс Зенона)

И всё же, мы движемся. С бесконечностью я планирую бороться бесконечностью. Конечно, между 0 и 1 простирается бесчисленное число точек. Но если двигаться со скоростью две бесконечности в секунду (каким-то неведомым способом!), то можно преодолеть эту дистанцию за полсекунды.

Дистанция состоит из бесконечных точек, движение возможно, поэтому движение описывается “бесконечностями точек в секунду”.

Вместо того, чтобы мыслить разностями (“Как далеко до следующей точки?”), мы можем сравнивать темпы (“Как быстро вы движетесь по множеству?”).

С виду покажется странным, но вы можете представить 10/5 как “Мне нужно пройти 10 ‘бесконечностей’ за 5 промежутков времени. Чтобы это осуществить, я буду проходить 2 ‘бесконечности’ за каждую единицу времени”.

Вывод: представляйте деление как темп движения по множеству точек.

А что после нуля?

И еще один взрыв мозга: Какое число идет после нуля? 0.01? 0.0001?

Хм.. Что бы вы ни назвали, я всегда смогу назвать меньше (Я просто разделю ваше число пополам….и все!).

Даже если мы не можем вычислить число после нуля, оно же должно быть там, правда? Оно как демоны древности – “его нельзя изображать, дабы оно не поразило тебя”.

Давайте обозначим расстояние от нуля до следующего меньшего числа “dx”. Я не могу точно сказать, насколько это большое расстояние, но оно есть!

Вывод: dx — это “прыжок” к следующему числу в множестве.

Точность измерений зависит от измерителей

Производная предсказывает изменение. Хорошо, и как измерить скорость (изменения в расстоянии)?

Полицейский: Вы знаете, с какой скоростью передвигались?

Водитель: Без понятия.

Полицейский: 150 километров в час.

Водитель: но я не ехал целый час!

Это точно, нам не нужен “полный час”, чтобы измерить вашу скорость. Мы можем измерить расстояние “до и после” (например, спустя 1 секунду) и получить вашу текущую скорость. Если вы прошли 41.7 метра за секунду, то скорость вашего движения составляет 150 км/ч. Всё просто, не так ли?

Не совсем. Представьте себе видеокамеру, присоединенную к Кларку Кенту (альтер-эго Супермена). Камера запечатлевает 24 картинки/секунду (40 мс на каждое фото), и Кларк кажется неподвижным. Если смотреть посекундно, он не движется, его скорость равна 0 км/ч.

Опять неверно! Между каждым фото за те 40 мс Кларк превращается в Супермена, расследует преступления и возвращается в свое кресло для невинного фотоснимка. Наши датчики зафиксировали скорость в 0 км/ч, но он на самом деле движется — просто движется слишком быстро, так, что наши приборы не успевают это уловить.

Вывод как в случае с камерой, которая следит за Суперменом, измеряемая скорость зависит от измерительного прибора!

Испытание на беговой дорожке

Мы уже видим суть производной на горизонте, все еще смутно, но видим! Нам нужны измерения до и после движения, чтобы зафиксировать изменения. Но эти измерения могут врать.

Представьте Деда Мороза без рубашки на беговой дорожке (да, постарайтесь, это нелегко). Мы будем измерять его пульс во время стресс-теста: мы присоединим к нему кучу тяжелых, холодных электродов и заставим его бежать.

Дед мороз пыхтит в поте лица, его пульс достигает 190 ударов в минуту. Должно быть, это его пульс в “условиях стресса”, верно?

Нет. Видите ли, присутствие строгих ученых и холодные электроды заставили его переживать, участив тем самым сердцебиение! Мы измерили 190 ударов в минуту, но кто знает, что мы увидим, когда уберем всё эти электроды? Конечно, если бы их не было, мы бы не смогли зафиксировать пульс. Как же быть? Давайте посмотрим на эту систему:

• значение измерения = фактическое значение + эффект измерения

Ух, спустя годы исследований, мы выяснили, что “каждый электрод прибавляет к фактическому пульсу еще 10 ударов в минуту”. Мы снова делаем замер (который снова показывает цифру в 190) и вычитаем влияние электродов (“идеальная оценка”).

Вывод: убираем “эффект электрода” после выполнения измерений.

Между прочим, “эффект электрода” проявляется везде. Исследования вывели Хоторнский эффект, при котором люди меняют свое поведение, потому что их изучают. Видимо, по этой причине красотки, постоянно находящиеся под вниманием парней, ударяются в разные диеты!

Понимание производной

Вооружившись всеми этими мыслями, мы можем понять, каким образом изменяется модель производной:

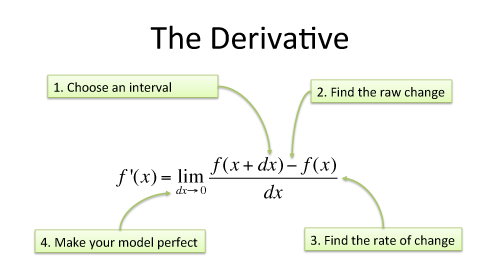
1. Выберите интервал
2. Вычислите конечное изменение
3. Найдите коэффициент изменения
4. Сделайте модель идеальной

Начните с изучения какой-то системы, f(x):

1. Изменяйте её с наименьшим возможным шагом (dx)
2. Получите разность “до и после”: f(x + dx) – f(x)
3. Мы точно не знаем, насколько мало “dx”, но нам и не важно: высчитайте коэффициент движение по множеству: [f(x + dx) - f(x)] / dx
4. Этот коэффициент, сколько мал он ни был, всё равно вызывает ошибку (наши камеры слишком медленно работают!). Представьте себе, что было бы, когда измерения идеальны, когда там нет никакого dx.

Вся магия происходит на последнем шаге: как нам убрать электроды? Есть два подхода:

• Пределы: что происходит, когда dx сводится к полному “ничто”, за пределами любой допустимой погрешности?
• Бесконечно малые величины: А что, если dx совсем крошечное число, которое невозможно зафиксировать ни в одной числовой системе?

Оба способа позволяют сформулировать идею того, “Как мы можем избавиться от dx, если оно не нужно нам?”.

Это моя любимая мозоль: Пределы — понятие современное, не существовавшее во времена Ньютона. Они позволяют “начисто” убрать dx. Но изучать их перед производными, это все равно, что показать человеку руль без автомобиля! Этот инструмент помогает производной работать, но не является отдельной темой для изучения.

Пример: f(x) = x²

Давайте распутаем клубок непонимания на простом примере. Как изменяется функция f(x) = x² по мере продвижения в непрерывном множестве?

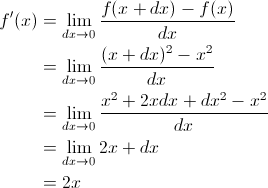
Заметьте разницу в двух последних частях уравнения:

• в одном погрешность обусловлена dx
• в другом происходит “реальное” изменение, dx=0 (наши измерения наконец не влияют на результат)

Настало время реальных чисел: Вот значения для f(x) = x² с интервалом dx = 1:

• 1, 4, 9, 16, 25, 36, 49, 64…

Абсолютная разница между результатами равна:

• 1, 3, 5, 7, 9, 11, 13, 15…

(В данном случае абсолютная разница — это “скорость” между каждым шагом вычислений с интервалом 1)

Рассмотрим скачок от x=2 к x=3 (3² – 2² = 5). Из чего сделала это значение “5″?

• Измеренный показатель= Фактический показатель + Погрешность
• 5 = 2x + dx
• 5 = 2(2) + 1

Ну конечно, мы измерили “передвижение на 5 точек в секунду”, потому что мы перескочили с 4 на 9 за один интервал.

Но наши инструменты нас обманывают! Единицы скорости вызваны реальным изменением, и 1 единица вызвана некачественными измерителями (1.0 — это довольно большой скачок, не так ли?).

Если мы ограничим себя только целочисленными значениями, 5 — очень даже неплохой показатель скорости между 4 и 9. Нет “погрешности” в предположении, что dx = 1, потому что это настоящий интервал между ближайшими точками.

Но в реальном мире, измерения каждую 1.0 секунду — это очень медленные измерения. А что если наш dx равен 0.1? Какую скорость мы замеряем на x=2?

Итак, вычисляем разницу между x=2 и x=2.1:

• 2.1² – 2² = 0.41

Запомните, 0.41 — это то, насколько ситуация изменилась за интервал, равный 0.1. Наша скорость от точки к точке составляет 0.41 / 0.1 = 41 (предполагая, что каждая точка — это целое число).

И, как прежде, у нас:

• Измеренный показатель= Фактический показатель + Погрешность
• 4.1 = 2x + dx

Интересно. При dx=0.1, измеренное и фактическое значения очень близки (4.1 и 4.2, погрешность 2.5%). При dx=1, измеренные значения серьезно разнятся (5 и 4, погрешность 25%).

Следуя этой мысли, можно четко понять, что выбросив электроды (полагая, что dx=0), мы получаем фактическое значение 2х.

Простыми словами: мы проанализировали, как f(x) = x² изменяется, нашли “неидеальное” измерение и вывели “идеальную” модель изменений — 2х.

Производная — это “непрерывное деление”

Интеграл видится мне как усовершенствованное умножение, где к одной изменяющейся величине можно применить другую.

Производная — это “улучшенная версия деления”, где скорость движения по множеству можно определить в любой момент. Что-то вроде 10/5 = 2 говорит: “у вас постоянная скорость по множеству, равная 2”. Когда по мере движения скорость меняется, нужно описывать скорость в каждый момент отдельно. Это и есть производная.

Если применить эту изменяющуюся скорость к каждому моменту движения, вы воспроизведете настоящее поведение в системе, точно как трейдеры применяют ежедневные изменения на фондовом рынке для воссоздания полной истории динамики цен. Но, это уже тема для совсем другой дискуссии.

Я понял: Как много значений у “производной”

Вы узнаете “производную” во многих контекстах:

• “Производная от x² равна 2x” означает “В каждой точке мы изменяемся со скоростью 2х (на значение, вдвое большее текущему значению х)”. (Общая формула изменений)
• “Производная равна 44” означает “В данном положении на множестве, наш коэффициент изменения равен 44. “При f(x) = x² в точке x=22 значение функции изменяется на 44 (частный коэффициент изменения).
• “Производная равна dx” ссылается на крошечный, гипотетический прыжок к следующей точке. Технически, dx — это “дифференциал”, и тут мы подмечаем, что запутались в терминах. Иногда люди будут говорить “производная х” и подразумевать dx.

Уяснил: Наша модель может быть неидеальна

Мы построили “идеальную” модель, делая изменения и улучшая её. Но иногда этого недостаточно. Делая прогнозы без dx, не всегда можно просчитать шаги наперед. Некоторые нерегулярные функции ломают всю идиллию: есть существенная разница между избавлением от dx с помощью предела и тем, что на самом деле происходит в тот момент. Эти функции называются “прерывистыми”, и это означает, что их “нельзя смоделировать с помощью пределов”. Как вы уже догадываетесь, производные на них не работают, потому что поведение таких функций невозможно предугадать.

Прерывные функции редко встречаются на деле, и на них очень часто ловят в тестах (“Ой, ты попытался взять производную от прерывной функции, глупенький, ты проиграл”). Представьте теоретические ограничения производных, а затем представьте их практическое применение в измерении разных явлений природы. Почти каждая функция, которая вам встретится (синус, косинус, е, полиномы и т.д.) будет непрерывной.

Понял: Интегралов вообще-то не существует

Связь между производными, интегралами и первообразными довольно тонкая (Я и сам поначалу не так её понял). Вот вам метафора. Начните с тарелки, это будет вашей функцией для изучения:

• Дифференцирование — это когда мы разбиваем тарелку на осколки. Мы вычисляем разницу, находим коэффициент изменения и предполагаем, что dx не существует.
• Интегрирование — это взвешивание осколков: изначально функция была “вот такой” большой. Это кумулятивная функция (суммирования масс осколков), она выдаст массу тарелки, но никогда не даст понять, как выглядела тарелка до разбития.
• Поиск первообразной — это попытки узнать, какой формы была тарелка, исходя из имеющейся кучки осколков.

Нет алгоритма по поиску первообразной — мы можем только строить догадки. Мы строим таблицу подстановки из известных производных (целая тарелка => кучка осколков), и ищем кучку осколков, похожую на нашу. “Давайте найдем интеграл 10х. Ну, похоже 2х — это производная x². Так что… каляки-маляки…10х — это производная от 5х².”.

Поиск производных — это целый механизм; поиск первообразных — это искусство. Иногда мы попадаем в тупик: мы берем изменения, по кусочками применяем их, и механически воссоздаем образ. Это может и не быть той “настоящей” тарелкой, но она будет достаточно хорошей для использования.

Еще одна тонкость: не являются ли интегралы и первообразные одним и тем же? (Я так обычно и думал).

Да, но это не совсем очевидно. Это всё равно, что сказать “А не будут одинаковы ли a² + b² и c²? Да, но только лишь в частном случае, когда речь идет о теореме Пифагора”.

Читая математику

Математика — это язык, и я хочу “читать” исчисления (не декламировать их вслух, как средневековые германские песнопения, а именно понимать). Моим самым крупным открытием было понимание нестабильности роли dx: он нужен для измерений, но мы избавляемся от него, чтобы создать идеальную модель. Пределы/бесконечно малые величины — это формализм, мы не можем опираться на них слишком. Ньютон, похоже, неплохо справлялся без них.

Освоив вышеперечисленное, хочется углубиться и в другие математические вопросы:

• Как можно измерить разные размеры бесконечности? (в каком-то смысле они все “бесконечны”, а в другом смысле интервал (0.1) явно меньше интервала (0.2))
• Какие реальные правила избавления от dx? (Как на самом деле работают пределы и бесконечно малые величины?)
• Как мы опишем числа без записывания их на бумагу? “Число, следующее за 0” — для начала нужно освоить это (я сам хочу изучить).

Основы интересны, когда ты реально понимаешь, почему они существуют. Приятных вычислений!

Перевод статьи «Calculus: Building Intuition for the Derivative»