Совершенно очевидно, что в круге 360 градусов, не так ли?
А вот и нет. Большинство из нас совершенно не понимают, почему в круге 360 градусов. Мы запоминаем это магическое число как «размер окружности», а затем, изучая физику или высшую математику, удивляемся всем этим «радианам».
«Радианы делают математику проще!» — так говорят математики; вот бы они еще научились конкретнее объяснять, в чем заключается простота (чтобы и мы чувствовали себя в дискуссиях на тему рядов Тейлора, как рыба в воде). Сегодня мы откроем, что на самом деле представляют собой радианы, и поймем, почему именно они делают математику проще.
Откуда берутся градусы?
До чисел и языка слов у нас были звезды. Древние цивилизации использовали астрономию для определения времен года, предсказания будущего и задабривания богов (если уж приносить в жертву богам людей, то лучше делать это в правильное время).
И как всё это относится к углам? Попробуйте разгадать: не странно ли то, что в окружности 360 градусов, а в году 365 дней? И с чего это вдруг созвездия в течение года совершают оборот на небосклоне?
Спорим, вы не сможете определить время года по картине ночного неба? Вот созвездие Большой Медведицы, видимое в 2008 году из Нью-Йорка:
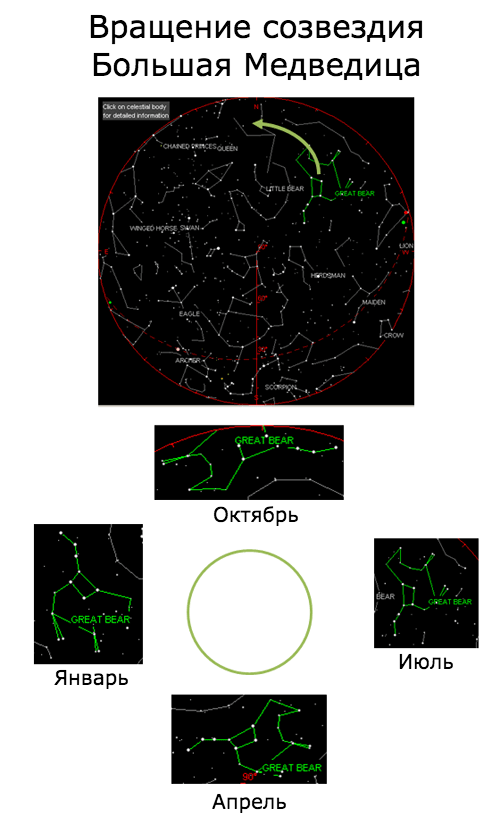
Созвездия каждую ночь немного продвигаются по кругу. Если Вы будете смотреть на небо в одно и то же время (например, в полночь), то заметите, что созвездия совершают полный круг по небу в течение года. Вот теория о возникновении градусов:
- Люди заметили, что за год созвездия совершали полный круг
- Каждый день они отодвигались совсем на немножно (это и есть «градус»)
- Поскольку в году около 360 дней, то и в круге было 360 градусов.
Но, есть одно но… Почему бы не сделать 365 градусов в окружности?
Простим древним эту погрешность: они пользовались солнечными часами, и не знали, что за год должно было набежать ровно 365.242199 градусов или дней, как вам теперь известно.
360 — достаточно точная цифра для тех времен. Она отлично согласуется с Вавилонской 60-ричной системой счисления, а также отлично делится (на 2, 3, 4, 6, 10, 12, 15, 30, 45, 90… ну вы поняли).
Математические расчеты по Солнцу выглядят вполне уместными
Земле везет: ~360 — отличное количество дней в году. Но эта цифра выглядит довольно субъективно: на Марсе у нас было бы ~680 градусов в окружности, так как марсианский год длится дольше (и сам марсианский день также длится дольше, как вы понимаете). В некоторых странах Европы люди пользуются градами, при которых круг приходится делить на 400 частей.
Многие из объяснений сходятся к следующему: «Ну, градус — довольно субъективная мера, но нам нужно было выбрать какое-то число». Не сейчас: далее мы увидим, что же на самом деле скрывают градусы.
Радианы спорят с градусами
Градус — это то, насколько мне, стоя в центре стадиона, приходится повернуть голову, чтобы увидеть человека, бегущего по беговой дорожке.
Представьте, что вы заметили друга, бегущего по огромному кругу:
— Привет, как далеко ты добежал?
— Ну, пробежался я нехило, около 10 километров.
— Ты что, совсем? Как сильно я повернул свою голову, чтобы тебя увидеть?
— Что?
— Я поясню словами покороче для непонятливых. Я в центре круга. Ты бежал вокруг. Насколько… я… повернул… свою… голову?
— Придурок.
Эгоистично, не так ли? Вот как вся эта математика построена! Мы пишем уравнения по типу «Слушай, как сильно я повернул свою голову, чтобы увидеть движущуюся планету/маятник/колесо?» Я уверен, что вы никогда не думали о том, что чувствует, о чем мечтает и на что надеется маятник. Это эгоистичный подход. Не кажется ли вам, что уравнения должны быть простыми не только для зрителя, но и для самого бегуна?
Радианы: скажи эгоизму нет
Многие вещи из физики (да и из жизни!) заставляет нас вылезти из своей привычной системы координат и посмотреть на вещи с другой точки. Вместо того, чтобы вычислять поворот своей головы, задумайтесь, как далеко продвинулся бегун.
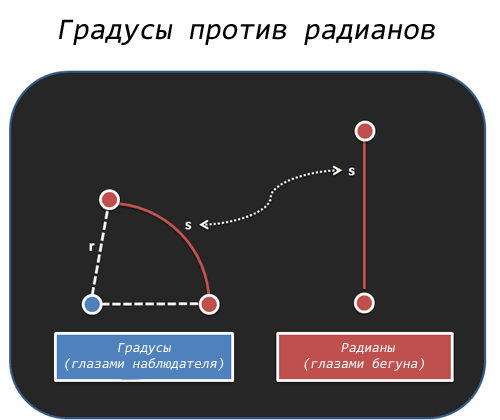
Градусы измеряют уголы по повороту головы. А радианы измеряют углы по пройденной дистанции.
Но само по себе расстояние не особо полезно, так как дистанция в 10 км может состоять из разного количества кругов, всё зависит от длины самого круга. Так что мы делим пройденную дистанцию на радиус круга, чтобы получить приведенный угол:

Вы часто будете встречать эту же формулу в таком виде:
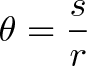
угол в радианах (тета) — это длина дуги (s), поделенная на радиус (r).
Окружность описывает 360 градусов или 2π радиан — пройти весь круг будет 2*π* r / r. То есть, радиан — это примерно 360 /(2 * π) или 57.3 градусов.
Надеюсь, вы не будете думать, как я: «Ну вот, еще одна непонятная единица. 57.3 — такое странное число». Оно странное только потому, что вы всё еще думаете о себе!
Пройти 1 радиан (единицу) — вполне себе нормальная дистанция для путешествия.
Другими словами, наш «чистый, ровный угол в 90°» означает то же, что и непонятные π/2 единицы для пройденного бегуном пути. Подумайте об этом: «Эй, парень, а не пробежишь ли ты для меня еще 90°? Сколько это? А, ну да, для тебя это будет π/2 километра». Для бегуна дистанция в градусах выглядит также странно, как и поворот в радианах для зрителя.
Радианы в математике — это как бы поставить себя на место другого: передвинуть свою точку зрения с поворота головы на движение бегуна.
Что в имени тебе моем?
Радианы — это единица измерения движения по кругу, характеризуемого радиусом. Я думаю, слово «радиан» иллюстрирует как раз связь с радиусом движения.
По сути, радианы — это такие же числа, как 1.5 или 73, без каких либо единиц измерения (в формуле «радианы = пройденный путь / радиус» длина делится на длину, так что любые единицы измерения сокращаются).
Но, говоря практическим языком, мы не математические роботы, так что проще думать о радиане как о «пути», пройденному по единичной окружности.
Использование радиан
Я пока и сам привыкаю думать радианами. Но мы уже довольно близко подобрались к понятию «дистанции бегуна»:
- Мы используем «вращений в минуту», а не «градусов в секунду» при измерении определенных угловых скоростей. Это ближе к точке зрения бегуна («Как много кругов он уже намотал?»)
- Когда спутник движется вокруг Земли, мы понимаем его скорость как «километров в час», а не «градусов в час». Разделите эту скорость на расстояние от земли к спутнику, и вы получите орбитальную скорость в радианах в час.
- Синус, эта замечательная функция, определяется в радианах, как:
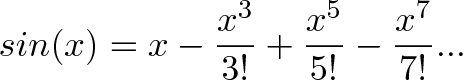
Эта формула работает, только если х представлен в радианах! Почему? Синус непосредственно связан с пройденным путем, а не с поворотом головы. Но мы отложим эту беседу до следующего раза.
Пример 1: Колеса автобуса
Давайте попробуем разобрать реальный пример: у вас есть автобус с колесами, радиус которых 2 метра (это автобус в стиле монстр-трак). Я скажу, как быстро вращаются колеса, а вы мне скажете, как быстро едет автобус. Готовы? «Колеса вращаются со скоростью 2000 градусов в секунду». Вы думаете:
- Хорошо, колеса вращаются на 2000 градусов в секунду. Это значит, они делают 2000/360 или 5 и 5/9 оборота в секунду. Длина окружности = 2*π*r, так что автобус движется со скоростью, эм, 2 * 3.14 * 5 и 5/9… где же мой калькулятор…
«Колеса проходят 6 радиан в секунду». Вы подумаете:
- Радианы — это длина единичной окружности, мы просто масштабируем эту величину согласно реальному радиусу, чтобы рассчитать, как далеко мы уедем. 6 * 2 = 12 метров в секунду. Следующий вопрос.
Вау! Никаких сумасшедших формул, никакого π — просто умножаем, чтобы конвертировать угловую скорость в линейную. А всё потому, что радианы говорят на языке движущегося тела.
Обратное действие также простое. Предположим, что мы несёмся 30 метров в секунду по автостраде (108 км/ч) на 24-дюймовых колесах (радиус которых равен 30 см). Как быстро вращаются колеса?
Ну, 30 метров в секунду / 0.3 м радиуса = 100 радианов в секунду.
Это было просто.
Пример 2: sin(x)
Пришло время для примера помощнее. Выберите число градусов (х) и вычислите значение sin(x) в калькуляторе:
Когда вы берете х очень маленьким, вроде 0.01, sin(x) тоже становится маленьким. И отношение sin(x)/x будет около 0.017 — что это означает? И еще страннее, что означает деление или умножение на градусы? Можно ли иметь квадратные или кубические градусы?
Радианы нас спасут. Зная, что они отвечают за пройденную дистанцию (это не просто пропорция!), мы можем интерпретировать уравнение таким образом:
- х — это то, как далеко вы прошли по кругу
- sin(x) — это то, как высоко вы взобрались по нему
- Так что sin(x)/x — это отношение того, как высоко вы находитесь, к тому, как далеко вы прошли: количество энергии, которое ушло в направлении «вверх». Если вы двигались вертикально, то это отношение будет равно 100%. Если вы двигались горизонтально, то равенство будет давать 0%.
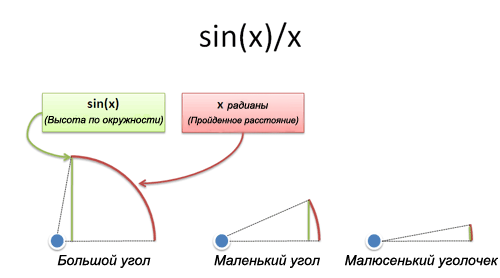
Когда что-то пододвигается на крошечное расстояние, как 0 или 1 градус с прежнего места, оно движется практически вверх. Если вы шагнете еще на меньшее расстояние, например с 0 до 0.00001 градуса, то вы действительно пройдете прямо вверх. Пройденное расстояние (х) очень близко к высоте (sin(x)).
Чем меньше х, тем ближе отношение к 100% — больше движения происходит вверх.
Радианы помогают увидеть, интуитивно, почему sin(x)/x стремится к 1 по мере уменьшения х. Мы просто топчемся на крошечном отрезке пути вверх. Между прочим, это также поясняет, почему sin(x) ~ x для маленьких чисел.
Конечно, вы можете точно доказать это с помощью калькулятора, но мышление радианами помогает вам это понять.
Запомните, эти связи работают только при измерении углов радианами. С градусами вы сравниваете высоты на окружности (sin(x)) с тем, насколько какой-то зритель поверную свою голову (х градусов).
Так в чем же смысл?
Градусы занимают свое место в нашей жизни. Нам ведь важно знать, насколько надо повернуть телескоп, развернуть сноуборд или покрутить рулем? По законам природы мы наблюдаем за тем, как движутся другие. И радианы больше подходят тем, кто движется, чем тем, кто за ними наблюдает. У меня ушло много лет на то, чтобы понять:
- Градусы выбраны произвольно, так как они основываются на солнце (365 дней ~ 360 градусов), но они как бы идут от обратного, потому что описывают процессы с точки зрения наблюдателя.
- Радианы описывают движение с точки зрения самих его участников, и поэтому «всё стает на свои места». Конвертировать угловую скорость в линейную довольно просто, и идеи вроде sin(x)/x приобретают смысл.
Даже углы можно рассматривать с более, чем одной точки зрения. Понимание радиан делают математические и физические формулы более осмысленными.
Приятных вычислений!
Перевод статьи «Intuitive Guide to Angles, Degrees and Radians»

