Частные производные для маркетинга

Функция нескольких переменных

Как понимать уравнение с несколькими переменными? Как количество свободы зависимой переменной!



В уравнении y = x+1 переменная y зависит от переменной x, такое количество свободы переменной y мы можем обозначить как 1 степень свободы. Переключатель, расположенный внизу, можно представить в виде уравнения с одной степенью свободы:

Состояние рычага можно определить с помощью переменной X и уравнения y=x+1.

Представим, что при y>0 переключатель включен, при y<0 переключатель выключен.

x > 0 рычаг включен (x=2, y=3)
x < -1 рычаг выключен (x=-2; y=-1)

Мы используем изменения только X для того, чтобы получить состояние этой системы, значит у этой системы количество степеней свободы = 1.

А теперь попробуем представить объект с несколькими степенями свободы, который может изменяться в разных измерениях. Фантазия рисует черные дыры, но все прозаичнее, это лампа!

Состояние это настольной лампы мы уже не сможем определить с помощью только одной переменной.



У нашей лампы три степени свободы, её состояние можно записать уравнением вида
l = x + y + z.

Чем больше количество независимых переменных, тем больше степеней свободы!

А что с производными?

Напомню, что производная — это скорость изменения функции, она имеет размер и направление (может расти или убывать). Определяется как предел отношения приращения функции к приращению аргумента, то есть насколько круто вверх или вниз пойдет функция y(x) при бесконечно малом приращении x. Мы находимся в исследуемой точки функции и делаем маленьких шажок вперед, нас ждет подъем или спуск? Насколько крут он будет?

Представим себе, шарик, который стоит на листе фанеры:


Эта ситуация хорошо иллюстрирует случай функции с  одной переменной, с одной степенью свободы.

Зеленый шарик можно представить как исследуемый объект. Если фанера стоит ровно, то производная равно 0, положение шарика не меняется.

Если фанера наклонена вниз:





То производная отрицательная, и функция уменьшается со скоростью тем большей, тем больше угол наклона вниз.


Если фанера наклонена вверх:




В этом случае производная положительна и функция растет со скоростью тем большей, чем больше угол наклона вверх.

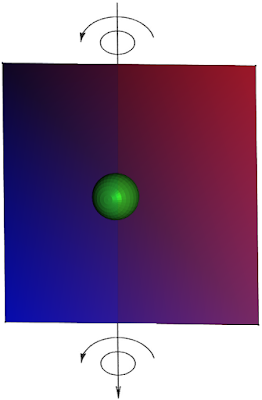
А теперь давайте добавим еще одну степень свободы и мы получим шарик на … плоскости!

Для определения двух степеней свобод можно использовать аналогию с осями вращения, по которым происходит наклон плоскости.


Таким образом мы можем провести горизонтальную ось вращения для X. Наклон плоскости по X определяется горизонтальной осью. Если угол наклона отрицательный, то шарик скатится в синюю область, а если положительный, то в красную. При нулевом наклоне шарик стоит на месте.




А ось вращения по Y вертикальная. При отрицательном угле наклона шарик катится на синюю область, при положительном на красную, при нулевом — стоит.




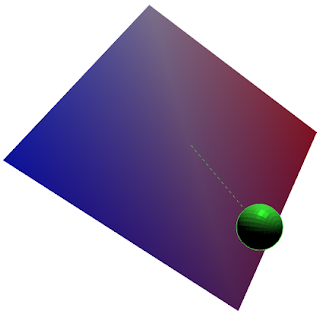
А теперь совместим две оси вращения по X и Y вместе:


Если наклоны по Y и X отрицательны, то у шарика нет шансов скатится на красную область, а если положительны — на синюю. Другое дело, если углы наклонов различны.

Таким образом мы вплотную подошли к понятию частных производных.

Для демонстрации возможностей создадим математическую модель процесса с двумя степенями свободы, которая описывается уравнением с двумя переменными:


Эта модель может упрощенно описывать вывод на рынок новый вид товара.

Поподробнее рассмотрим нашу модель:

5x² — эта наша прибыль, чем дольше мы работаем тем больше продаем, наша прибыль растет. Здесь x² можно рассматривать как площадь охвата аудитории, чем дольше работаем, тем больше о нас знают.

А выражение —500 × ln(y) — а это наша расходы на маркетинг, на рекламу. Чтобы вывести что-то новое на рынок нужно проявить усилие, и сильнее всего усилие на старте, когда про наш товар еще никто не знает.

В нашей модели переменные X и Y означают время, можно рассматривать их как количество месяцев с начала работы.

Давайте попробуем с помощью математического анализа функции многих переменных ответить на вопрос: Через какое время можно ожидать рост?

Рассмотрим нашу модель через частные производные:


В нашей математической модели: 5x² — 500 × ln(y) нам необходимо получить частные производные по X и по Y. При вычислении частных производных по одной переменной другая считается константой, а производная константы равна нулю.

Таким образом:

Производная по X = 10x
Производная по Y = -500/y

Полным дифференциалом функции называется главное линейное приращение функции в данной точке, то есть углы наклона по нашим осям.

Рассмотрим точку (X;Y) = (1;1), состояние нашей модели после первого месяца работы.

Полный дифференциал нашей функции 10x — 500/y будет равняться 10 × 1 — 500/1, то есть 10 — 500. Можно легко посчитать углы наклона нашей плоскости по осям.

Учитывая, что производная — это тангенс наклона касательной, то углы можно высчитать через обратную функцию арктангенс:

Арктангенс 10 = 84.28 градусов наклон по X
Арктангенс -500 = -89.88 градусов наклон по Y

Это означает, что шарик на плоскости скатится в синюю область:




Функция убывает! Мы несем убытки!

Вычислим момент, когда функция перейдет в рост.

Для этого вычислим вторую производную для функции 5x² — 500 × ln(y).

Первая производная = 10x - 500/y

Вторая производная (производная от первой) = 10 — 500/y²

В точке перехода от убывания к росту скорость функции будет равна нулю. Действительно, если мы идем вперёд, то для того, чтобы пойти назад мы должны остановиться, хотя бы на мгновение. Температура воздуха при смене с положительной на отрицательную проходит через ноль.

Чтобы узнать в какой точке скорость меняет направление, приравняем вторую производную к нулю.

10 — 500/y² =0

тогда -500/y² = -10

1/y² = 500/10

1/y² = 10/500

1/y² = 1/50

y ~ 7.07

Тогда полный дифференциал нашей функции будет равен:


Что соответствует одинаковому углу наклона плоскости по осям, шарик лежит ровно на
 центре, между положительной и отрицательной областями - производная равна нулю.

А в точке 7+1 = 8 наша плоскость примет положительный наклон.

Ведь полный дифференциал будет 80 - 62.5.

Что дает:
Арктангенс 80 = 89.28 градусов наклон по X
Арктангенс -62.5 = -89.07 градусов наклон по Y


В точке (9;9) положительный наклон горизонтальной оси X будет еще больше.

Для наглядности посмотрим на график нашей функции:





Действительно примерно с 7.07 график переходит в рост. Все правильно! С 7 месяца работы мы растем!

Сейчас по рассмотрели скорость изменения функции в направлении синхронного приращения и X, и Y (1;1); (2;2); (3;3). Это упрощение позволило нам рассмотреть базовые принципы частных производных.

В следующей раз мы научимся находить скорость измнения функции двух переменных в любом направлении, и научимся определять направления наибольшей скорости, для этого нам придется внести понятия производной по направлению и градиента функции.