Несмотря на целых два курса линейной алгебры, все мои знания о ней состояли из «матриц, определителей, чего-то там собственного».
Почему так? Давайте разберемся в особенностях моего курса:
- Название курса «Линейная алгебра», но почему-то упор делается на термины вроде матриц и векторов
- Суть обучения сводилась к порядку строк/колонок с мнемоникой вместо пояснения самого смысла происходящего
- Предпочтение отдавалось абстрактным примерам (2-мерные векторы! 3-мерные векторы!), и до самой последней недели мы всячески избегали примеров из реального мира
В таком тяжелом бою между терминологией и смыслом выживают только физики, графические программисты и прочие мазохисты. Мы упустили главный момент:
Линейная алгебра предоставляет вам мини-таблицы для математических уравнений.
Можно взять таблицу данных (матрицу) и создать обновленные таблицы на ее основе. В этом и есть сила таблицы вычислений, написанной в виде уравнения.
Мне бы очень помогло такое введение в линейную алгебру на своем курсе, с пояснением на примере фондовой биржи из реального мира.
Что в имени тебе моем?
«Алгебра», грубо говоря, означает, «связи». Алгебра в начальной школе раскрывает связи между неизвестными числами. Не зная x и y, мы все равно можем узнать, что (x + y)2 = x2 + 2xy + y2
«Линейная алгебра» означает, в общем смысле, «линейно-подобные связи». Тут остановимся поподробнее.
Прямые линии предсказуемы. Представьте себе, будто вы идете по крыше: поднимитесь на три метра вверх по склону, и вы подниметесь ровно на 1 метр над уровнем земли (Вы же движетесь по склону! Вертикальный подъем/пройденный путь = 1/3). Пройдите 6 метров, и вы уже подниметесь над землей на целых 2 метра. Сравните подъем по крыше со взбиранием по куполу: каждый метр, пройденный по горизонтали, поднимает вас на разную высоту над землей.
Линии очень милые и предсказуемые:
- Если 3 метра вперед подымают на 1 метр, тогда пройденный путь длиной в 10х раз больше должен поднять вас над землей на 10х высоту (30 метров пути дают 10-метровый подъем)
- Если 3 метра, пройденных по крыше, подымают человека на 1 метр над землей, а 6 метров пути дают подъем на 2 метра, тогда (3 + 6) метров пути должны подымать на (1 + 2) метра
Выражаясь математическим языком, операция F является линейной, если масштабирование исходных параметров масштабирует ее значение:
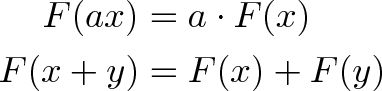
В нашем примере, F(x) вычисляет подъем при движении вверх по склону крыши на x метров, и сохраняются такие соотношения:
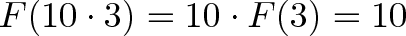
Линейные операции
Операция — это вычисление, основанное на некоторых входных параметрах. Какие операции являются линейными и предсказуемыми? Похоже, операция умножения как раз хороший пример.
Экспоненты (F(x)=x2) не являются предсказуемыми: 102 равно 100, но 202 равно 400. Мы удвоили входной параметр, но учетверили результат.
Вы удивитесь, но обычное сложение также нелинейно. Рассмотрим функцию «плюс три»:
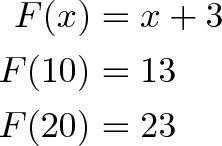
Мы удвоили аргумент (входное значение) и не удвоили результат. (Да, функция F(x) = x + 3 представляет собой уравнение прямой линии, но она всё равно не «линейная», потому что F(10) не равно 10*F(1). Забавно.)
Наша единственная надежда — умножение на константу: F(x) = ax (в нашем примере с крышей a=1/3). Тем не менее, мы всё еще можем комбинировать линейные операции для создания новой линейной операции:
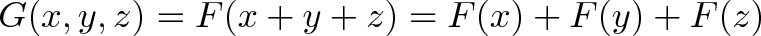
G состоит из 3 линейных кусочков: если мы удвоим аргументы, у нас удвоится значение самой функции.
Тут мы пустим в ход «мини-арифметику»: умножайте аргументы на константу и складывайте результаты. Это довольно полезный прием, потом что он позволяет разделить аргументы, проанализировать их индивидуально, а затем сложить результаты:
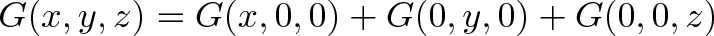
Если бы аргументы вели себя как экспоненты, разделить их не получилось бы — тут следует анализировать всё сразу, а не по отдельности.
Организация аргументов и операций
Большинство курсов математики бросают вам в лицо детали матрицы. «Ну что ж, детишки, давайте научимся говорить. Берем существительное, глагол и прилагательное. Далее, спрягаем глагол. Затем добавляем предлоги…»
НЕТ! Суть не в грамматике. В чем заключается основная идея? Как пояснить суть процесса?
- У нас есть набор входных параметров для анализа
- У нас есть предсказуемые, линейны операции (наша «мини-арифметика»)
- Мы генерируем результат, возможно, снова его трансформируя
Хорошо. Для начала нам нужно отследить набор входных параметров? Как насчёт того, чтобы представить их в виде списка:
x y z
Неплохо. Мы бы могли написать то же самое в виде строки (x, y, z) — держитесь за эту мысль.
Далее, как же нам контролировать наши операции? Помните, у нас есть только «мини-арифметика»: умножения и конечное сложение. Если наша операция F ведет себя так:
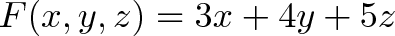
То мы бы могли сократить написание всей функции до (3, 4, 5). Мы знаем, что нужно умножить первый аргумент на первую цифру, второй аргумент на вторую и т.д. и сложить результат.
Нужен только первый аргумент?
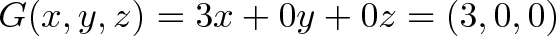
Давайте добавим остроты: как организовать множество наборов входных параметров? Допустим, мы хотим произвести операцию F над аргументами (a, b, c) и (x, y, z). Можно попробовать так:
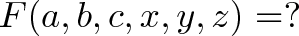
Но это не сработает: операция F работает только с 3 аргументами, а не с 6. Нужно разделить аргументы на группы:
1-я группа 2-я группа ------------------------- a x b y c z
Так-то лучше.
А как в таком случае прогнать один и тот же аргумент через несколько операций? Для каждой операции должна быть своя строка:
F: 3 4 5 G: 3 0 0
Как всё аккуратно. У нас вырисовывается структура: аргументы в вертикальных колонках, а операции в горизонтальных строках.
Визуализируем матрицу
В математике слов недостаточно. Я покажу, как визуализирую аргументы, операции и результаты:
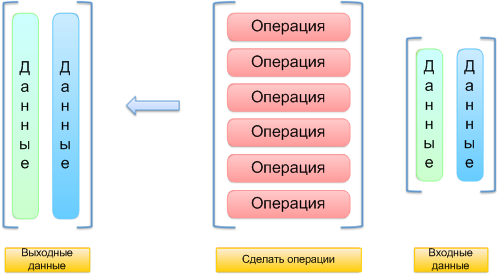
Представьте себе как будто вы «наливаете» каждый вводный параметр в каждую операцию:
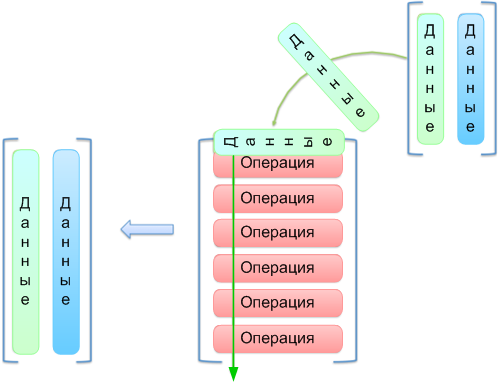
По мере прохождения аргумента через операцию создается результат (значение операции). В нашем примере аргумент (a, b, c) проходит через операцию F и выдает результат 3a + 4b + 5c. Затем он проходит через операцию G и образовывает результат 3a + 0 + 0.
Настало время красной таблетки. Матрица представляет собой условное обозначение наших диаграмм:
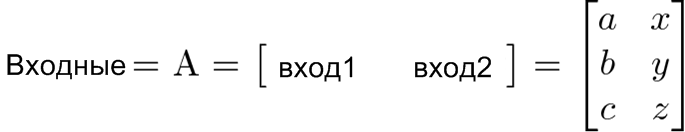
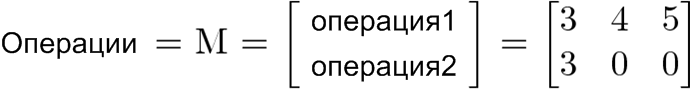
Матрица — это единая переменная, представляющая собой таблицу аргументов или операций.
Хитрость #1: Порядок чтения
Вместо последовательности аргумент => матрица => результат, мы используем запись вызова функции, например, y = f(x) или f(x) = y. Обычно матрица обозначается заглавной буквой (F), а одинарная колонка аргумента — маленькой буквой (х). Так как у нас есть несколько аргументов (А) и несколько результатов (В), их тоже рассматривают в качестве матрицы:
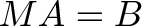
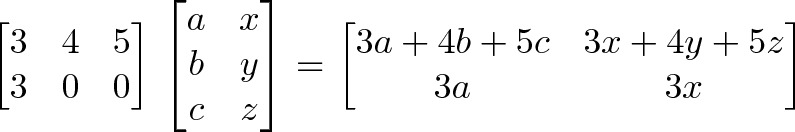
Хитрость #2: Нумерация
Размер матрицы измеряется как СxК: количество строк, количество колонок. Элементы в матрице обозначаются таким же образом: aij — элемент i-й строки j-й колонки (на доске «i» и «j» очень легко перепутать, глядя издалека). Мнемоника отлично запоминается с помощью контекста, и вот что мне приходит на ум:
- СК — сокращенно от «система координат» или «спортивный клуб»
- Для поиска нужного элемента матрицы двигайтесь по матрице по перевернутой букве Г ( или латинской букве L): сместитесь вниз на i, а затем вправо на j позиций
Почему представлять матрицу в виде СК имеет смысл? Матрица операций в нашем примере имеет размер 2×3, а матрица аргументов — 3×2. Если написать их вместе, получится:
[Матрица операций] [Матрица аргументов] [число операций x размер операций] [размер аргументов x количество аргументов] [m x n] [p x q] = [m x q] [2 x 3] [3 x 2] = [2 x 2]
Заметьте, что матрицы касаются «размера операций» и «размера аргументов» (n = p). Они должны быть равны! Если аргумент состоит из 3 компонентов, то операция тоже будет содержать 3 элемента. На самом деле, мы можем только умножать матрицы при n = p.
Матрица результатов содержит m строк операций для каждого аргумента, и q аргументов дает матрицу размером «m x q».
Более навороченные операции
Давайте освоим операции получше. Имея 3 аргумента, мы можем соорудить несколько 1-операционных матриц:
- Сумматор: [1 1 1]
- Усреднитель: [1/3 1/3 1/3]
«Сумматор» — это просто a + b + c. «Усреднитель» работает по принципу: (a + b + c)/3 = a/3 + b/3 + c/3.
Попробуйте эти 1-линейники:
- Есть только первый аргумент: [1 0 0]
- Только второй аргумент: [0 1 0]
- Только третий аргумент: [0 0 1]
Объединив всё это в одну матрицу, мы получим:
[1 0 0] [0 1 0] [0 0 1]
Ухты — да это же «единичная матрица», которая копирует 3 аргумента в 3 результата без изменений. А как насчёт такого варианта?
[1 0 0] [0 0 1] [0 1 0]
Он меняет местами аргументы: (x, y, z) становится (x, z, y).
А вот это?
[2 0 0] [0 2 0] [0 0 2]
А это уже удвоитель аргументов. Мы можем переписать его в виде 2*I (I — единичная матрица).
И да, если захотите представлять аргументы в виде координат вектора, матрица операций будет преобразовывать наш векторы. Вот несколько примеров:
- Масштаб: делает все аргументы больше/меньше
- Наклон: делает определенные аргументы больше/меньше
- Зеркальное отображение: аргументы становятся отрицательными
- Поворот: генерирует новые координаты на основе старых (восток стает севером, север — западом и т.д.)
Это всё геометрические интерпретации умножения и способы деформации векторного пространства. Просто помните, что векторы — это просто примеры данных, которые можно изменять.
Невекторный пример: портфель ценных бумаг
Давайте попрактикуем линейную алгебру в реальном мире:
- Аргументы: портфель ценных бумаг с долларами в акциях Apple, Google и Microsoft
- Операции: изменения в стоимости компаний вследствие выпуска новостей
- Результат: обновленный портфель
И бонусный результат: давайте создадим новый портфель, содержащий прибыль/потери от конкретного события.
Обычно мы бы отслеживали изменения в таблице. Но давайте научимся думать методами линейной алгебры:
- Входной вектор мог бы быть ($Apple, $Google, $Microsoft), показывая сумму в каждом виде акций. (Эти значения могут быть получены из другой матрицы, которая просто умножила количество акций на их цену. Представьте себе!)
- 4 операции для результата могут включать: обновить стоимость акций Apple, обновить стоимость акций Google, обновить стоимость акций Microsoft, вычислить прибыль
А теперь визуализируем задачу. Представьте себе проход по каждой операции:
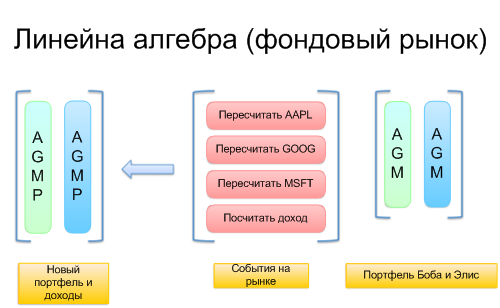
Тут важно понять, почему мы вообще строим такую матрицу, а не оперируем цифрами вслепую.
Давайте пройдемся по сценарию.
Допустим, выпустили секретный iDevice: акции Apple подпрыгнули на 20%, Google подешевели на 5%, а Microsoft остался на прежнем уровне. Мы хотим обновить стоимость каждой акции, используя нечто, похожее на единичную матрицу:
Новая цена Apple [1,2 0 0] Новая цена Google [ 0 0,95 0] Новая цена Microsoft [ 0 0 1]
Новая цена Apple представляет собой оригинальную цену, увеличенную на 20% (Google = 5% рост, Microsoft = без изменений).
Подождите! Нам же еще нужна совокупная прибыль:
Общая прибыль = (0,20 * Apple) + (-0,05 * Google) + (0 * Microsoft)
Конечная матрица операций имеет вид:
Новая цена Apple [1.2 0 0] Новая цена Google [ 0 0.95 0] Новая цена Microsoft [ 0 0 1] Общая прибыль [.20 -.05 0]
Вам стало понятнее? Три аргумента на входе, четыре значения на выходе. Первые три представляют собой «измененную копию», а четвертая представляет собой сумму всех изменений.
А теперь давайте выдадим портфели акций для Ани ($1000, $1000, $1000) и Пети ($500, $2000, $500). Мы можем посчитать всё вручную, а можем использовать Wolfram Alpha (расчёт):

(Примечание: Входные параметры должны быть представлены в колонках, но проще печатать их в виде строк. Операция Transpose (транспонирование), обозначенная буквой t (тау), конвертирует строки в колонки).
Конечные цифры: у Ани теперь акций AAPL на $1200, GOOG на $950, и MSFT на $1000, а совокупная прибыль составила $150. У Пети акций AAPL на $600, GOOG на $1900, и MSFT на $500, при совокупной прибыли $0.
Что происходит? Мы делаем вычисления в нашей таблице. Линейная алгебра появилась в 1800-х годах, а вот динамические таблицы были изобретены только в 1980-х. Я связываю такой огромный промежуток между этими двумя изобретениями с плохим преподаванием линейной алгебры.
Историческая справка: Решение системы уравнений
Ранним применением таблиц чисел (еще не «матриц») была запись систем линейных уравнений:
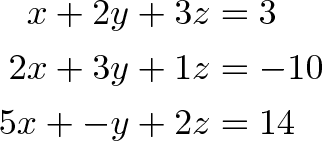
превращается в
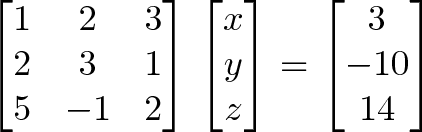
Можно попросту складывать/вычитать строки в матрице и выводе, вместо многочисленных переписываний полной системы уравнений. По мере того, как матрица преобразовывается в единичную матрицу, значения x, y и z появляются на стороне вывода.
Этот процесс, названный исключением по Гауссу-Жордану с выбором главного элемента, экономит время. Несмотря на это, линейная алгебра больше касается трансформаций матрицы, а не решения огромных систем уравнений (это всё равно что использовать Excel для составления списка покупок).
Терминология, определители, собственный вектор и число
У слов есть технические категории для описания их применения (существительные, глаголы, прилагательные). Матрицы можно разделить таким же образом.
Описания вроде «верхний треугольник», «симметричная», «диагональная» показывают форму матрицы. Они также влияют на ее возможные трансформации.
Определитель — это «размер» преобразования матрицы на выходе. Если вводным параметром был единичный вектор (представляет площадь размером 1), определитель — это размер трансформированной площади или объема. Определитель 0 означает, что матрица «деструктивная» и не может иметь обратную матрицу (это всё равно, что умножение на 0: информация попросту теряется).
Собственный вектор и собственное число представляют собой «оси» преобразования. Представьте себе, как крутите глобус: любая точка на глобусе кроме полюсов движется по своей траектории. «Собственный вектор» — это вводный параметр, который не изменяет направление при прохождении через матрицу (он расположен «вдоль оси»). И хотя направление не изменяется, размер может меняться. Собственное значение — это число, обозначающее, во сколько раз уменьшается или увеличивается собственный вектор при прохождении через матрицу.
(Тут моя интуиция слаба, и я бы хотел больше покопаться в теме. Вот красивая диаграмма и видео.)
Матрицы в качестве входных значений
Мы ведь можем использовать матрицы операций в качестве входных параметров!
Представьте рецепт как список команд (досыпьте два стакана сахара, три стакана муки…). А что, если нам нужна метрическая версия, применимая для любых дозировок продуктов? Сами инструкции воспринимайте как простой текст, а единицы конвертируйте в нужные. Рецепт — это не что иное, как «аргумент», который нужно изменить. После перевода всех единиц в нужные нам, можно снова последовать инструкциям и приготовить вкусняшку.
Матрица операций — это нечто похожее: набор команд, которые надо преобразовать. Применяя одну матрицу операций к другой, вы получите новую матрицу операций, в которой применяются оба преобразования, по порядку.
Если N — это «изменить портфель согласно новостям», а Т — «изменить портфель, вычтя налоги», то применение обоих операций записывается как:
TN = X
и означает «Создайте матрицу X, которая сначала изменяет портфель согласно новостям, а потом согласно налогам». И тут нам даже не понадобились входные данные по портфелям, мы просто применили одну матрицу к другой.
Красота линейной алгебры состоит в возможности представить целую таблицу вычислений одной буквой. Хотите применить одно и то же преобразование несколько раз? Используйте N2 или N3.
Скажите, пожалуйста, а можно использовать простое сложение?
Да, потому что вы очень вежливо попросили. Наша «мини-арифметика» кажется довольно ограниченной: умножение, но не сложение? Пора расширить рамки своего мышления.
Представьте добавление простой единицы в матрицу вводных параметров: (x, y, z) превращается в (x, y, z, 1).
Теперь в матрице операций появилось еще одно значения, с которым нужно поработать! Если мы хотим x + 1 , мы можем написать:
[1 0 0 1]
А x + y – 3 будет выглядеть так:
[1 1 0 -3]
Ну ничего себе!
Хотите эксцентричных пояснений? Мы представляем, будто бы наш аргумент существует в измерении на 1 порядок выше, и в этом измерении мы размещаем «1». Мы смещаем большую размерность, которая выглядит как наклонная плоскость в текущей размерности. Например, возьмите аргумент (x, y, z, 1) и пропустите его через:
[1 0 0 1] [0 1 0 1] [0 0 1 1] [0 0 0 1]
Результатом будет (x + 1, y + 1, z + 1, 1). Игнорируя 4-ю размерность, каждый входной аргумент получил +1. Можно продолжить добавлять измерения в матрицу и сгенерировать еще больше дополнительных плоскостей.
Мини-арифметика не такая уж и ограниченная.
Заглядывая наперед
Я опустил некоторые премудрости линейной алгебры, но не сильно переживаю на этот счёт. Почему? Эти метафоры помогают мне мыслить матрицами больше, чем все те курсы, которые я закончил «на отлично». Я, наконец, на вопрос «В чем польза от линейной алгебры?» я могу ответить теми же аргументами, «Почему полезны динамические таблицы?».
Они не несут никакой пользы, если только вам не нужен инструмент, способный решить любую задачу из реального мира. Поинтересуйтесь у бизнесменов, что они выберут: пожертвовать свою почку или навсегда лишиться Excel. Это и есть сила линейной алгебры, которую мы упустили при изучении в университете: удобная система обозначений, позволяющая привнести табличные вычисления в обычные математические уравнения.
Приятных вычислений!
Перевод статьи «An Intuitive Guide to Linear Algebra»

