Преобразование Фурье стало для меня одним из самых поразительных открытий. К моему сожалению, его чудесный смысл был похоронен за этими страшными уравнениями:
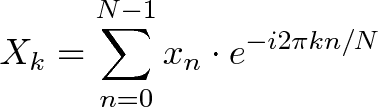
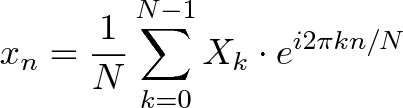
Да… Вот так выглядит определение преобразования Фурье. Но, вместо того, чтобы погружаться в непонятные формулы, давайте для начала поймем его смысл. Вот парочка простых метафор:
Что делает преобразование Фурье? Если дан вкусный коктейль, оно поможет отыскать рецепт его приготовления.
Как? Просто пропустит коктейль через фильтр ингредиентов и найдет нужные.
Почему? Состав проще анализировать, сравнивать и изменять, чем сам готовый коктейль.
Как снова получить коктейль? Просто смешать все ингредиенты в стакане.
А теперь более математическим языком:
Преобразование Фурье берет массив, изменяющийся во времени, измеряет каждый "ингредиент цикла" (величину, смещение и скорость вращения) и возвращает общий "рецепт цикла" (график частоты).
Настало время формул? Нет! Давайте немного покопаемся в живых примерах циклов и массивов.
Если всё пойдет хорошо, должен наступить момент озарения, и вы сами увидите, как рождается преобразование Фурье. Мы сохраним детальный математический анализ этого понятия для будущих поколений.
Это не марш галопом по формулам, это легкая прогулка по понятным местам, которую мне бы очень хотелось иметь во время учебы. Вперед!
От коктейль к рецепту
Математическое преобразование — это всего лишь изменения перспективы. Мы меняем наше понятие количества от "единичных элементов" (полосы на песке, торговля в рассрочку) на "группы из 10 элементов" (десятичные) в зависимости от того, что мы считаем. Счёт в матче? Считайте голы по одному. Умножение? Десятичными числами, пожалуйста.
Преобразование Фурье переносит наш взгляд с точки зрения потребителя на точку зрения изготовителя, меняя угол обзора с "Что я видел?" на "Как это было сделано?"
Другими словами: дан коктейль, давайте найдем его рецепт.
Почему? По рецепту очень легко сделать такой же вкусный коктейль, если снова захочется полакомиться. Чтобы описать, что вы пили, вам не нужно будет анализировать каждую каплю и выдавать результат, вы просто скажете "Я пил бананово-апельсиновый коктейль", и всем станет понятно, что в нем было. Рецепт проще категорировать, сравнивать и изменять, чем уже готовый объект.
Итак… дан коктейль, как же нам отыскать его рецепт?
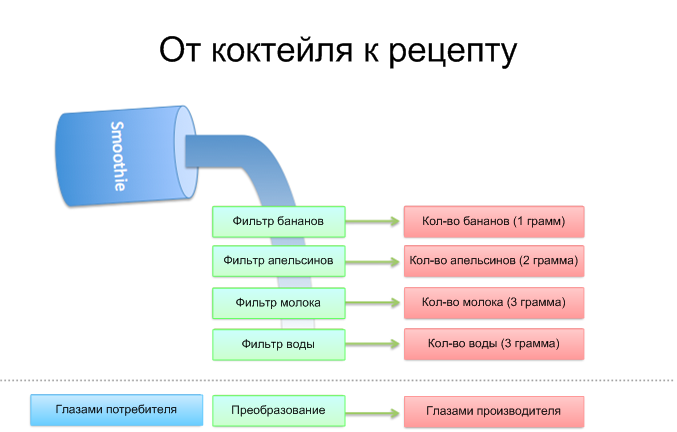
Представьте, что поблизости у вас есть несколько фильтров:
Вылейте коктейль через "банановый" фильтр. С его помощью отфильтровалось 30 граммов бананов.
Пропустите коктейль через "апельсиновый" фильтр. Он отфильтровал 60 граммов апельсинов.
Также пропускаем остаток через "молочный" фильтр. Целых 100 граммов молока!
И, наконец, "водяной" фильтр отделил 100 граммов воды.
В итоге ничего не осталось, мы отфильтровали все ингредиенты и можем воссоздать рецепт. В чем подвох?
Фильтры должны быть независимы друг от друга. Банановый фильтр должен выделать только бананы, и ничего другого. Добавление большей дозы апельсинов никак не должно влиять на считывание банановой составляющей.
Набор фильтров должен быть полным. Мы не получим настоящий рецепт, если упустим хотябы один ингредиентов ("Ой, тут же еще манго был!"). Набор фильтров должен отлавливать каждый ингредиент.
Ингредиенты должны быть совместимыми. Смузи можно разделить на составные части фильтрами и снова смешать без проблем (Печенье подойдет? Не очень. Кому нужны крошки в стакане?). Ингредиенты должны вести себя одинаково при смешивании и отделении.
Представляем мир как набор интервалов
Преобразование Фурье выдвигает интересную точку зрения: А что если любой сигнал можно было бы изобразить с помощью вращения (повторяющиеся интервалы)?
Ух, эта мысль просто взрывает мозг, и бедный Жозеф Фурье тоже вначале отбросил эту идею. (Действительно ли даже лестничную площадку можно представить в виде кругов?)
И не смотря на десятилетия споров в математическом сообществе, мы всё еще надеемся, что студенты усвоят эту сложную мысль без проблем. Ну да,конечно… Придется следовать интуиции.
Преобразование Фурье помогает найти рецепт сигнала, в точности как мы расправились с рецептом коктейль:
Начните с сигнала, изменяющегося во времени
Примените фильтры, чтобы измерить каждую возможную "круговую составляющую"
Соберите полный рецепт, чётко прослушав, сколько раз в сигнале встречается каждый выделенный "круговой ингредиент"
Стоп. В этом месте обычно большинство учебников начинаются забрасываться примерами применения. Не пугайтесь, но вы действительно узнаете много нового:.
Если вибрации землетрясения можно разделить на "ингредиенты" (вибрации разной скорости и силы), можно строить здания так, чтобы они не взаимодействовали даже с самыми сильными вибрациями.
Если звуковые волны можно также разделить на составляющие (нижние и верхние частоты), мы можем улучшить звучание тех составляющих, которые нас интересуют, и спрятать то, что нам не нужно. Звучание можно очистить от скрипа и различных случайных звуков. Возможно, схожие "звуковые рецепты" можно сравнить (что активно используется в сервисах распознавания звука).
Если цифровые данные можно представить в виде множества колебаний, самыми незначительными можно пренебречь. На этом принципе работает "компрессия с потерями", которая позволяет значительно уменьшать размер файлов (этот эффект поясняет, почему файлы JPEG и MP3 гораздо меньше в размере, чем файлы форматов .bmp и .wav).
Если радиоволна является нашим исследуемым сигналом, то мы можем использовать фильтр для прослушивания канала на определенной частоте. Представьте, что в мире-коктейль каждый человек обращает внимание на разные ингредиенты: Адам ищет яблоки, Даша ищет бананы, а Петя получает качан капусты (прости, друг).
Преобразование Фурье невероятно полезно в машиностроении, и можно привести массу готовых примеров. Но нам нужно добраться до самой сути, а не рассматривать готовый эффект. Так что, запаситесь терпением, идем дальше.
Думайте кругами, а не только синусоидами
Одной из моих крупнейших ошибок на пути понимания преобразования Фурье было разделение определений "синусоида" и "окружность".
"Синусоида" — это графическое представление множества повторяющихся данных (например, волны синуса или косинуса), и 99% времени она отображает движение в одном измерении.
"Окружность" — это круглое, двумерное множество, которое вы не раз видели на бумаге. Если вам нравится выражаться научно при объяснении элементарных вещей, вы бы назвали окружность "комплексной синусоидой".
Название пути по окружности "комплексной синусоидой" — это как назвать слово "мульти-буквой". Но в случае слов всё не так, как со коктейль или синусоидами: слово несет в себе смысл, который точно не состоит из смысла входящих в него букв.
Преобразование Фурье — это про круговые траектории (не 1-мерные синусоиды), и формула Эйлера — отличный способ сгенерировать одно такое преобразование:
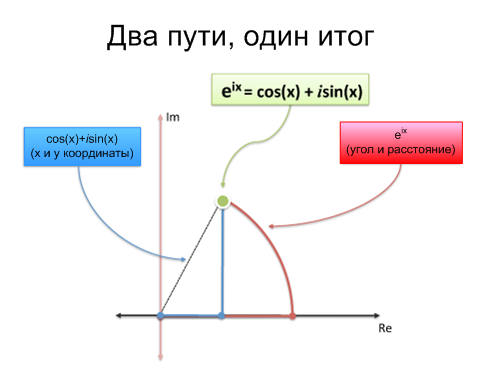
Должны ли мы использовать воображаемые экспоненты, чтобы двигаться в круге? Нет. Но это удобно и компактно. Мы можем разделить путь на реальную и воображаемую части, но не забывайте полную картинку: мы движемся по кругу.
Следуя круговой траектории
Допустим, мы болтаем по телефону и, как обычно, хотим нарисовать одинаковые окружности одновременно. Что мне нужно сказать вам?
Насколько большая окружность у нас будет? (Амплитуда, т.е. размер радиуса)
Как быстро нам нужно ее нарисовать? (Частота. 1 окружность в секунду представляет собой частоту в 1 Герц (Гц) или 2* радиан/сек)
Когда начнем? (Фазовый угол, где 0 градусов — это ось Х)
Я мог бы сказать "2-сантиметровый радиус, начинай на 45 градусах, 1 окружность в секунду, вперед!". Спустя полсекунды мы должны были оказаться в одной и той же точке: стартовая точка + пройденный путь = 45 + 180 = 225 градусов (на 2-сантиметровой окружности)
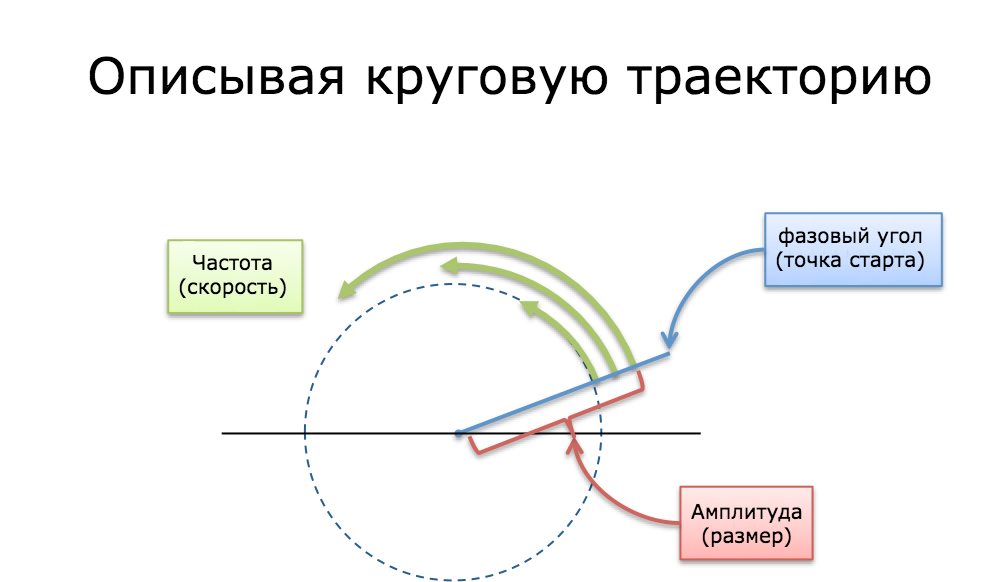
Любой круговой траектории нужен размер, скорость и стартовый угол (амплитуда / частота / фаза). Мы можем даже совмещать траектории: представьте крошечные автомобили, которые наматывают круги на разных скоростях.
Совместное положение всех циклов движения — это и есть наш сигнал, как, например, общий запах всех ингредиентов коктейль.
Ниже представлена симуляция базовой круговой траектории:
(Макет и начальный код основана на этой анимации, а это исходный код. Для нее вам потребуется современный браузер. Нажмите на график, чтобы поставить на паузу).
Величина каждого цикла указана по порядку, начиная с 0 Гц. Цикл [0 1] означает:
Величину, равную 0 для цикла 0 Гц (0Гц = постоянный цикл, который застрял на оси Х на нуле градусов)
Величину, равную 1 для цикла 1 Гц (проходит 1 цикл за каждый интервал времени)
Сейчас начнется самое сложное:
Синяя кривая отображает реальную часть цикла. Еще один милый математический трюк: реальная ось окружности, которая обычно указывается горизонтально, здесь показана на вертикальной оси. Вы можете мысленно прокрутить окружность на 90 градусов, если вам так удобнее.
Временные точки проставлены с наибольшей частотой. Сигналу в 1 Гц нужны две временные метки — в начале и в конце (одиночный замер не имеет частоты). Значения времени [1 -1] показывают амплитуду этих равномерно расположенных интервалов.
Вы всё еще со мной? [0 1] — это и есть 1-герцовый цикл.
Теперь давайте добавим цикл 2 Гц. [0 1 1] означает "Ничего на 0 Гц, мощность 1 на частоте 1 Гц, мощность 1 на частоте 2 Гц".
Ну и дела! Крошечные машинки совсем одичали: зеленые линии — это циклы на 1 и 2 Гц, а синяя линия — суммарный результат.
Мдаа, маленькие машинки потихоньку сходят с ума: зеленые линии описывают периоды в 1 Гц и 2 Гц, а синяя линия показывает общий результат. Попробуйте попереключать зеленый флажок, чтобы чётко увидеть конечный результат. Комбинированный "аромат" — это колебание, которое начинается на максимуме и спадает вниз на всей оставшейся части интервала.
Желтые точки — это отметки, где мы, собственно, измеряем сигнал. На 3 определенных циклах (0 Гц, 1 Гц, 2 Гц), каждая точка отмеряет ⅓ пути по сигналу. В данном случае циклы [0 1 1] генерируют временные значения [2 -1 -1], которые начинаются на максимуме (2) и спадают вниз (-1).
Ой! Мы же не можем забыть о фазе, начальном угле! используйте величину:угол, чтобы настроить фазу. То есть, [0 1:45] — это период в 1 Гц, который начинается на 45 градусах:
Это смещенная версия [0 1]. По времени мы получаем уже [0.7 -0.7] вместо [1 -1], потому что "края" нашего периода не совпадают с точками замеров, которые всё также находятся на средних точках.
Преобразование Фурье вычисляет набор скоростей периодов, мощностей и фаз для соответствия любому временному сигналу.
Наш сигнал становится абстрактным понятием, которое мы рассматриваем как "наблюдения в промежутке времени" или "составные части частотного диапазона".
Хватит разговоров: пора переходить к делу! В симуляторе укажите временной или интервальный массив, чтобы увидеть изменения на графике. Если это моменты времени, вы получите набор интервалов (которые формируют "волну"), который соответствует вашим желаемым точкам.
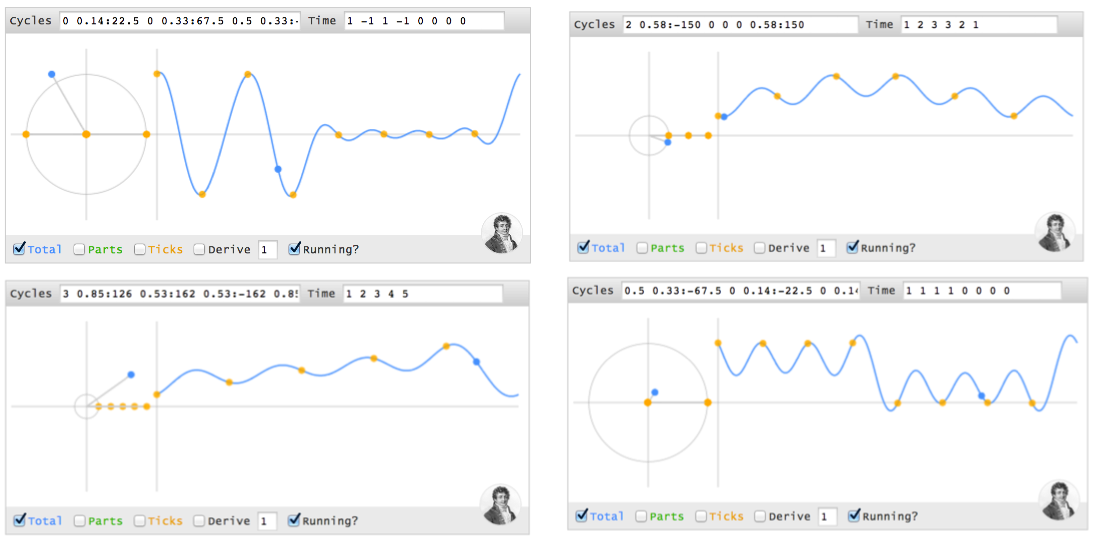
Но… правда у полученной волны какие-то странные значения между желтыми точками интервалов? Ну конечно. Разве кто-то утверждал, что сигнал во времени путешествует по прямым линиям, или кривым, или зигзагам в тех промежутках, где мы не ставим свои замеры? Сигнал ведет себя так, как нам нужно, только в равномерно расположенные моменты, в которых мы запрашиваем его характеристики.
Совершим скачок во времени
А можем ли мы сделать резкий скачок во времени, как, например, (4 0 0 0), используя циклы? (для обозначения временных точек я буду пользоваться круглыми скобками). Составляющие нашего периода должны начинаться в одну линию (на максимальном значении, 4), а затем "взрываться наружу". Все остальные точки будут равны нулю, и такой баланс кажется очень странным на фоне кучи других периодов сигнала, резвящихся вокруг (мы не можем просто "выключить" их). Давайте пройдемся по каждой временной точке:
В момент времени 0, каждый ингредиент периода имеет максимальное значение. Не учитывая другие временные точки, (4 ? ? ?) является суммой 4 периодов (0 Гц 1 Гц 2 Гц 3 Гц), амплитуда каждого сигнала — 1 и фаза 0 (т.е. 1 + 1 + 1 + 1 = 4).
На каждой последующей точке (t=1, 2, 3), сумма всех сигналов обнуляется.
Вот такой фокус: когда два периода находятся на противоположных сторонах окружности (север и юг, восток и запад, и т.д.), их сумма равна нулю (3 периода могут в сумме давать ноль, если они равномерно распределены на 0, 120 и 240 градусах)
Представьте совокупность точек, передвигающихся по окружности. Вот позиция каждого сигнала в каждой точке времени:
Время 0 1 2 3 ------------ 0 Гц: 0 0 0 0 1 Гц: 0 1 2 3 2 Гц: 0 2 0 2 3 Гц: 0 3 2 1
Заметьте, что период 3 Гц начинается с 0, доходит до 3, затем значение подымается до "6" (но позиций всего 4, а 6 модуль 4 = 2), затем значение "9" (9 модуль 4 = 1).
Когда период длиной всего 4 единицы, скорость движения на середине периода (2 единицы) будет либо равномерной (разность 0, 4, 8…) или располагаться на противоположных сторонах (разница of 2, 6, 10…).
Ну что ж, давайте остановимся детальее на каждой временной точке:
Время равно 0: Все сигналы принимают максимальное значение (в сумме 4)
Время равно 1: 1 Гц и 3 Гц в сумме дают 0 (позиции 1 и 3 являются обратными друг другу), 0 Гц и 2 Гц также обнуляются в сумме.
Время равно 2: 0 Гц и 2 Гц принимают значение 0, в то время, как 1 Гц и 3 Гц имеют значение 2 (на противоположной стороне). Сумма по-прежнему равна 0.
Время равно 3: 0 Гц и 2 Гц обнуляются, также 1Гц и 3 Гц в сумме дают ноль.
Время равно 4: (повторение t=0): Все сигналы сходятся в одну точку.
Вся суть в том, что сигналы в сумме обнуляются на разных частотах (0 Гц и 2 Гц, 1 Гц и 3 Гц), или же обнуляются в паре (0 Гц + 2 Гц и 1 Гц + 3 Гц).
Когда каждый сигнал имеет одну и ту же амплитуду в фазе 0, всегда на начале периода сигналы будут равны, а затем обнуляться в сумме в определенный момент времени (сумма их значений будет равна нулю). Кстати, у меня нет пока что достойного обоснования этому явлению, но вы сами можете увидеть. Попробуйте [1 1], [1 1 1], [1 1 1 1], а также такие скачки времени: (2 0), (3 0 0), (4 0 0 0)).
Вот как я визуализировал начальную позицию, за которой следует суммарное обнуление:
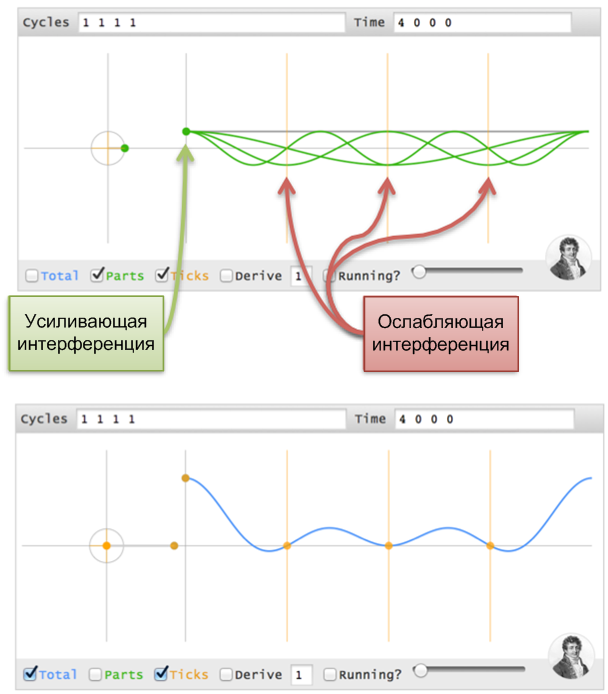
Двигаем скачок времени
Далеко не всё всегда происходит на отметке t=0. Можем ли мы передвинуть наш временной скачок, сделав примерно так — (0 4 0 0)?
Похоже, что составные части периода должны быть такими же, как и при (4 0 0 0), но сигналы должны уравниваться на t=1 (одна секунда в будущем). И тут на поле вступает фаза сигналов.
Представьте себе гонку с 4 бегунами. В нормальных гонках все бегуны стартуют на одной линии, случай (4 0 0 0). Скучно как-то.
А если я хочу, чтобы все бегуны финишировали одновременно? Это легко устроить. Просто передвиньте бегунов вперед-назад на соответствующую дистанцию друг от друга. Бабуля может начать бег за пару метров до финишной линии, Усэйн Болт начнет за 100 м до старта, и финишную прямую они пересекут рука об руку.
Изменения фазы, начального угла, представляют собой не что иное, как задержки в периоде сигнала. Вот как мы настроим начальную позицию, чтобы задержать каждый период на 1 секунду:
Сигнал с частотой 0 Гц никуда не движется, так что он уже выровнен.
1 Гц сигнал проходит 1 кружок за целые 4 секунды, так что 1-секундная задержка представляет собой четверть полного оборота. Смещение фазы — 90 градусов назад (-90) и он доходит до фазы = 0, до своего максимального значения в момент t=1.
Сигнал с частотой 2 Гц вдвое быстрее, так что дайте ему вдвое больший угол покрытия (-180 или 180 градусов).
Сигнал 3Гц втрое быстрее, так что ему нужно дать втрое большую дистанцию для пробега (-270 или +90 градусов).
Если временные точки (4 0 0 0) проставлены на сигналах [1 1 1 1], то временные точки (0 4 0 0) имеют [1 1:-90 1:180 1:90]. (Примечание: Я использую "1 Гц", но имею в виду "1 полный цикл сигнал проходит за 1 целый временной период").
Теперь понятие "цикл" тоже стало осмысленным!
Визуализация этого варианта временного скачка такая же, не считая того, что все сигналы уравниваются на t=1.
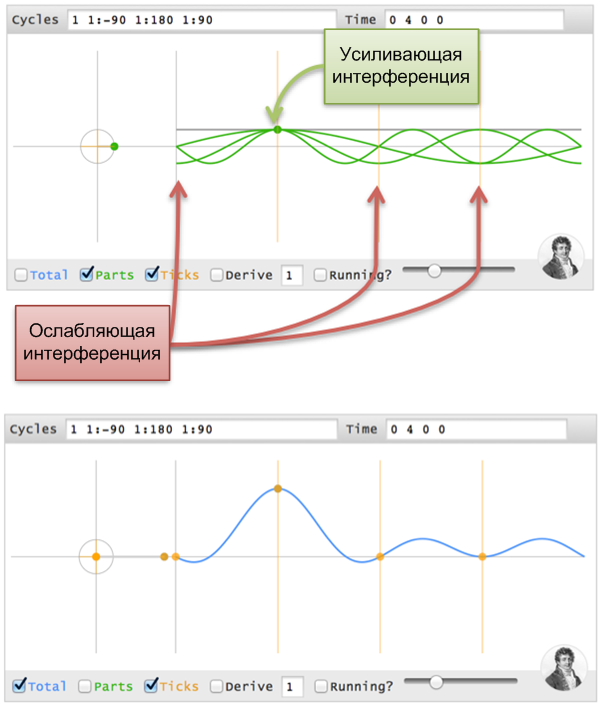
Проверьте свою интуицию: Можете ли вы сделать (0 0 4 0), т.е. 2-секундную задержку? При 0 Гц нет фазы. 1 Гц имеет 180 градусов, 2 Гц — 360 (или 0), а 3Hz — 540 (или 180), так что получится [1 1:180 1 1:180].
Открытие полного преобразования
Большое откровение: наш сигнал – это не что иное, как совокупность скачков во времени! Если мы объединим "рецепты" каждого скачка времени, то получим рецепт полного сигнала.
Преобразование Фурье выстраивает рецепт почастотно:
Разделяет полный сигнал (a b c d) на "временные скачки": (a 0 0 0) (0 b 0 0) (0 0 c 0) (0 0 0 d)
Для любой частоты (например, 2 Гц), предварительный рецепт будет а/4 + b/4 + c/4 + d/4″ (сила каждого скачка разделена между всеми частотами)
Подождите! Нужно сместить каждый скачок согласно задержке по фазе (угол для "1-секундной задержки" зависит от частоты).
Фактический рецепт для частоты = a/4 (без смещения) + b/4 (1 секунда задержки) + c/4 (2 секунды задержки) + d/4 (3 секунды задержки).
Мы можем затем пройтись по каждой частоте, чтобы получить полное преобразование.
Вот как выглядит переход от "математического русского" к чистой математике:
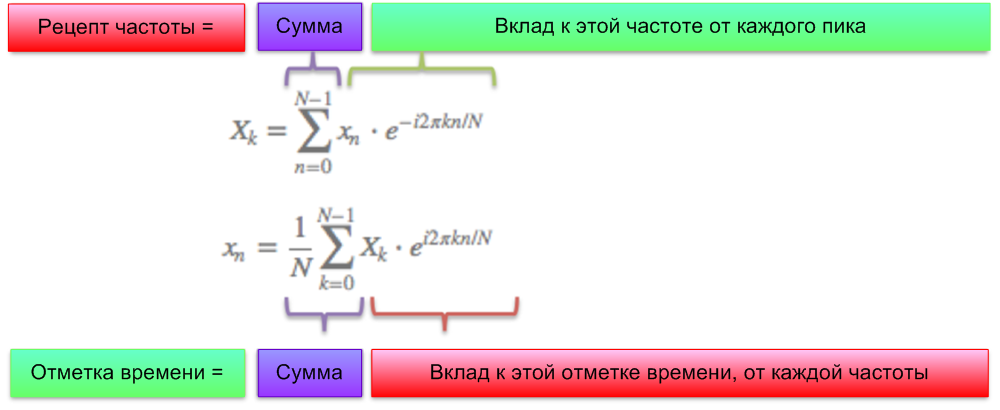
Пара комментариев:
N = число временных выборок
n = текущая выборка, которую мы рассматриваем (0 .. N-1)
xn =значение сигнала в момент времени n
k = текущая частота, которую мы рассматриваем (0 Герц до N-1 Герц)
Xk =количество частоты k в сигнале (амплитуда и фаза, комплексное число)
Множитель 1/N обычно ведет к обратному преобразованию (от частот назад ко времени). Это разрешается, хотя я предпочитаю 1/N в прямом преобразовании, так как он дает фактические значения на временных скачках. Вы можете пойти дальше и использовать 1/sqrt(N) в обоих преобразованиях (в прямом и обратном случаях всё равно присутствует множитель 1/N).
n/N – это процент времени, через которое мы проходим. 2 * pi * k — это скорость в радианах / сек. e^-ix — это наш обратный путь по окружности. Комбинация того, как далеко мы продвинулись для этих скорости и времени.
Расчёты по преобразованию Фурье сводятся к "суммированию комплексных чисел". Многие языки программирования не поддерживают комплексные числа напрямую, поэтому их нужно преобразовывать в прямоугольные координаты, и суммировать их.
Приложение: Проектирование на циклы
У Стюарта Риффла есть отличная интерпретация преобразования Фурье:

Чтобы найти энергию на определенной частоте. вращайте свой сигнал по окружности этой частоте, и найдите среднее значение на точках по пути.
Представьте вращение вашего сигнала в центрифуге и проверку угла наклона. У меня есть поправка: мы должны вращать в обратном направлении (экспонента в уравнении нуждается в знаке минуса). Вы уже знаете, почему: нам нужна фазовая задержка, чтобы скачки появлялись в будущем.
Приложение: Еще одна роскошная визуализация
Лукас Виейра, автор замечательных анимаций для Википедии, также вдохновился на создание интерактивной анимации:
(Детальный список опций управления)
Преобразование Фурье основывается на циклах, прибавляемых к циклам, которые прибавляются к циклам. Попробуйте сделать "скачок во времени", настроя мощность на 1 для каждого компонента (нажмите Enter после ввода каждого числа). Забавный факт: при наличии достаточного количества параметров, можно нарисовать любую фигуру, даже Гомера Симпсона.
Перевод статьи «An Interactive Guide To The Fourier Transform»

