Или разложение пропорций на составные множители
Пропорции — это краткое изложение сценариев с числами, как, например «заработок в день». К сожалению, полученный результат от такой пропорции совершенно скрывает процесс своего появления.
Например, посмотрим, какая выручка у этих двух предприятий:
- Картинная галерея «Пассаж» продает по одной картине в день, стоимостью 10000 рублей.
- Рыбзавод «Приморье» продает 10 форелей в день, 1000 рублей каждая.
Но если посмотреть на общую ежедневную прибыль, то она одинакова у обоих предприятий — 10000 рублей в день, верно?
А вот как на самом деле ведутся дела у этих двух предприятий:

Транзакции — это рабочие лошадки, которые приносят доход, но почему-то они не упоминаются в описании «рублей в день». В данном случае одна транзакция — это продажа одной картины или одной форели. При изучении этого понятия лучше разделять результат на 2 составляющих: энергию и частоту.
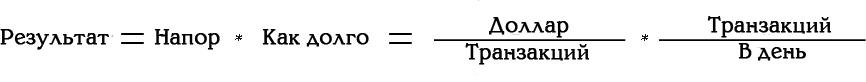
С энергией и частотой я теперь четко вижу два отдельных рычага для роста. Пропорция рублей/день наталкивает на мысли вроде: «Для лучших результатов, мне нужно улучшиться на 1/день… это означает, что мне стоит укоротить день?… Как это возможно? Аааа, это, наверное, означает просто отрезок дня, требующийся на осуществление одной транзакции…».
Зачем усложнять? Перепишите пропорцию так, чтобы она четко отражала суть: Что такое «Энергия», и как «Часто» мы ее получаем?
Лошадиная сила, крутящий момент, об/мин
В физике мы определяем обыденные понятия вроде «мощности» формальным соотношением:
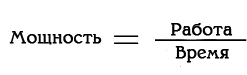
Ну, хорошо. Мощность модно пояснить пропорцией, но мы же уже включили обратный режим мышления, так что превратим формулу в произведение:
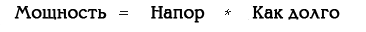
Так кажется проще. Но что могут в данном случае означать «Энергия» и «Частота»?
«Сила» — это, вероятно, та работа, которую мы делаем (например, поднимаем штангу), а «Частота» — это то, как часто мы это делаем (сколько раз вы поднимаете ее?).
За одну минуту Павел поднял 50 кг 10 раз, а Ксюша умудрилась поднять 500 кг один раз. Из этого уравнения получается, что Павел и Ксюша имеют одинаковую мощность (хотя, если честно, я больше боюсь Ксюшу). Механик по двигателям расшифровывал бы мощность так:
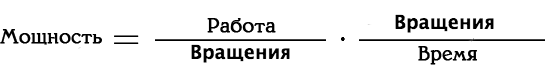
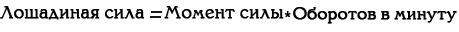
Что всё это означает?
- Крутящий момент — это та же «Энергия», или как много веса (и как далеко) может быть передвинуто одним оборотом двигателя (например, передвижение 500 кг веса на 1 метр)
- Об/мин (оборотов в минуту) — это как часто вращается двигатель
Двигатель мотоцикла создан для оборотов, т.е. для быстрого вращения колес. Ему не нужен большой крутящий момент — достаточно просто толкать сам мотоцикл и парочку пассажиров, но эту силу нужно посылать на колеса снова и снова. То есть в формуле мощности мотоцикла ключевым параметром будет именно об/мин (чем чаще вращаются колеса, тем дальше уедет мотоцикл).
Бульдозер же больше создан для «Энергии», ему нужно проламывать тяжелые стены, ворочать камни. И тут не нужно слишком часто махать ковшом, так как одна разрушенная стена в минуту — уже отлично, и более чем достаточно.
Я не физик и не автомобилист, но как минимум могу осмыслить соотношение Энергии и Частоты в различных случаях.
Шестерни могут изменять соотношение между Энергией и Частотой в одном конкретном двигателе. Если вы движетесь вверх по дороге, борясь с гравитацией, чего нам стоит прибавить? Или же, если вы плывете по ровной автостраде? Пытаетесь тронуться со стоянки? Едете по скользкому снегу? Потеряли тормоза и хотите как-то замедлить автомобиль? Энергия/Частота всегда заставляет меня думать интуитивно, а вот Работа/Время — нет.
Вариация: Электроэнергия
Электроэнергия имеет такую же пропорцию, как и механическая мощность:
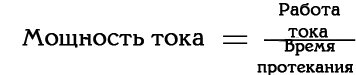
Ой, простите. Снова неясно, что это означает. А как насчёт:
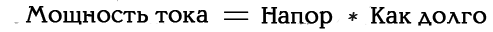
Очень сложно сразу понять, что к чему, но можно представить что-то (крошечный двигатель?), что движет Энергию по кругу внутри провода. Если мы назовем это «заряд», тогда получим:

И мы даже можем дать этим отдельным дробям свои формальные названия:
- Напряжение (Энергия): Как много работы совершает каждый заряд
- Ток (Частота): Как быстро заряды движутся по проводу
Ну и теперь уже знакомая нам формула:
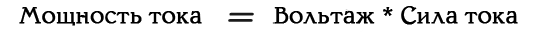
Вот это да! Я не силен в электричестве, но, как минимум, моя цель ясна: найти аналогии, где напряжение означает «Энергию», а ток — «Частоту».
И мы можем еще попробовать свои силы в интуитивном мышлении: когда вас зимой бьет током дверная ручка, это Энергия или Частота постаралась? Какой атрибут нужно увеличить батареям? Что будет лучше для движения электроэнергии по линиям электросети? (Да здравствует сопротивление!)
В то время, как пропорции считают, что любой тип мощности сводится к расчёту «Работа/Время», вариант «Энергия/Частота» заставляет нас задумываться и о других составляющих процесса, таких как Крутящий момент / Об/мин в одном случае и Напряжение/Ток в другом.
Что на самом деле происходит? Это параметры, детка.
Точка зрения «Энергия/Частота» возвращает нас к исходным параметрам пропорции. Вместо рублей и дней мы задаемся вопросом, как отдельная транзакция влияет на исход дела:
- Можем ли мы увеличить размер каждой транзакции?
- Можем ли мы увеличить количество транзакций на каждый день?
Формальными терминами, Мы представили новый параметр для пояснения взаимодействия. Чтобы изменить пропорцию с a/b на пропорцию, параметризированную по x, мы можем сделать следующее:
![]()
Можно изменить точку обзора, чтобы увидеть x как ключевой компонент. В математике мы часто сменяем точку обзора для того, чтобы упростить задачи:
- Вместо того, чтобы спрашивать, что случится с наблюдателем, можем ли мы изменить параметры и спросить, что он видит? (Градусы против радиан)
- Можем ли мы видеть огромную функцию как параметризированную меньшими? (Цепное правило — правило дифференцирования сложной функции)
- Можем ли мы представлять вероятности в виде дробей, а не процентов? (Это упрощает теорему Байеса).
Игра с параметрами — это способ преобразовать непонятную идею в понятную, ту, которая работает именно для вас. Поскольку я не думаю обычно перевернутыми понятиями, я для себя упростил этот процесс: использую два умножения вместо деления.
Приятных вычислений!
Перевод статьи «Understand Ratios with "Oomph" and "Often"»

